
分析 发现:(1)当PN∥y轴时,点N距x轴的最近,根据已知条件得到PN=$\frac{1}{2}$MN=3$\sqrt{3}$,于是得到点N距x轴的最近距离为9-3$\sqrt{3}$,此时∠APN=90°,求得t=$\frac{90}{15}$=6,于是得到PA的长为6;
(2)当t=9时,得到∠APN=180°-9×15°=45°,AP=9×1=9,设此时直线MN交y轴于点D,根据三角函数的定义得到AD=AP•tan45°=9×1=9,即可得到结论;
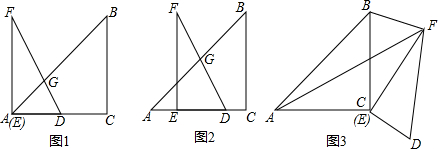
(3)如图1,当点P在直线l上时,过点P作PH⊥x轴,垂足为H,根据三角函数的定义得到OQ=3$\sqrt{3}$+t,求得t=11,根据角的度数即可得到结论;
拓展:如图2,设直线l与AB交于点E,与半圆P相切于点T,解直角三角形得到PT=3$\sqrt{3}$,AE=AP+PE=t+6,过点E作EF⊥x轴,垂足为F,求得OQ=6+3$\sqrt{3}$+t,列方程得到t=8,即可得到结论;
探究:设直线l与AB交于点G,与半圆P相切于点R,解直角三角形得到PR=3$\sqrt{3}$,AG=AP-PG=t-6,过点G作GJ⊥x轴,垂足为J,解方程得到t=14,于是得到结论.
解答 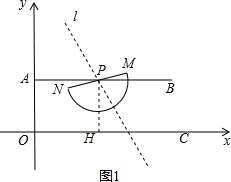 解:发现
解:发现
(1)当PN∥y轴时,点N距x轴的最近,
∵A(0,9),
∴OA=9,
∵MN=6$\sqrt{3}$,
∴PN=$\frac{1}{2}$MN=3$\sqrt{3}$,
∴点N距x轴的最近距离为9-3$\sqrt{3}$,
此时∠APN=90°,
∴t=$\frac{90}{15}$=6,
∴PA的长为6;
故答案为:9-3$\sqrt{3}$,6;
(2)MN所在直线经过原点,
理由:当t=9时,∠APN=180°-9×15°=45°,AP=9×1=9,
设此时直线MN交y轴于点D,
则AD=AP•tan45°=9×1=9,
又OA=9,
所以点D与点O重合,即MN所在直线经过原点;
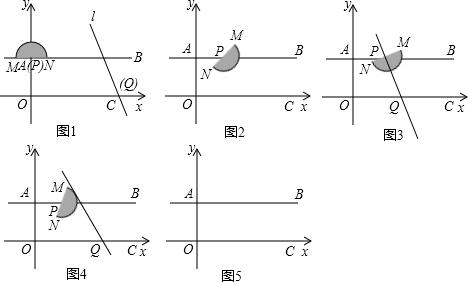
(3)如图1,
当点P在直线l上时,过点P作PH⊥x轴,垂足为H,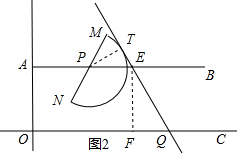
∴OQ=OH+QH=AP+$\frac{PH}{tan60°}$=t+$\frac{9}{\sqrt{3}}$=3$\sqrt{3}$+t,
∴CQ=t,
∵OQ+CQ=3$\sqrt{3}$+t+t=OC=22+3$\sqrt{3}$,得t=11,
此时,∠APN=180°-11×15°=15°,
∠NPQ=180°-15°-60°=105°,
∠MPQ=180°-105°=75°,
∴S左:S右=105:75=7:5;
拓展
如图2,设直线l与AB交于点E,与半圆P相切于点T,
则PT=3$\sqrt{3}$,PE=$\frac{PT}{sin60°}$=$\frac{3\sqrt{3}}{\frac{\sqrt{3}}{2}}$=6,AE=AP+PE=t+6,
过点E作EF⊥x轴,垂足为F,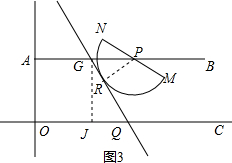
则OQ=OF+FQ=AE+$\frac{EF}{tan60°}$=(t+6)+$\frac{9}{\sqrt{3}}$=6+3$\sqrt{3}$+t,
CQ=t,
由OQ+CQ=6+3$\sqrt{3}$+t+t=OC=22+3$\sqrt{3}$,得t=8,
此时,点P的坐标为(8,9);
探究
当半圆P在直线右侧,且与直线l相切时,如图3所示,
设直线l与AB交于点G,与半圆P相切于点R,
则PR=3$\sqrt{3}$,PG=$\frac{PR}{sin60°}$=$\frac{3\sqrt{3}}{\frac{\sqrt{3}}{2}}$=6,AG=AP-PG=t-6,
过点G作GJ⊥x轴,垂足为J,
则OQ=OJ+JQ=AG+$\frac{GJ}{tan60°}$=(t-6)+$\frac{9}{\sqrt{3}}$=3$\sqrt{3}$-6+t,
CQ=t,
由OQ+CQ=3$\sqrt{3}$-6+t+t=OC=22+3$\sqrt{3}$,得t=14,
则直线l与半圆P有公共点的时间为14-8=6秒.
点评 本题考查了圆的综合题,圆心角,解直角三角形,平移和旋转的性质,切线的性质,正确的作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2)且tan∠ABC=$\frac{1}{2}$;
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2)且tan∠ABC=$\frac{1}{2}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
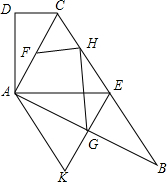 如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com