
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| b |
| 2a |
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| b |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么
如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么| AD |
| AB |
| A、0.618 | ||||
B、
| ||||
C、
| ||||
| D、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
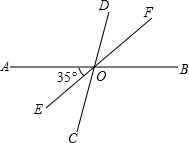 直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF
直线AB,CD相交于O,过点O画射线OE,OF,已知∠AOE=35°,∠EOC=∠DOF查看答案和解析>>
科目:初中数学 来源: 题型:
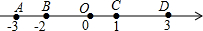 定义:若数轴上A、B两点分别对应数a、b,则A、B两点之间的距离记作|AB|,|AB|=|a-b|,根据图中信息,完成下列各题:
定义:若数轴上A、B两点分别对应数a、b,则A、B两点之间的距离记作|AB|,|AB|=|a-b|,根据图中信息,完成下列各题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com