
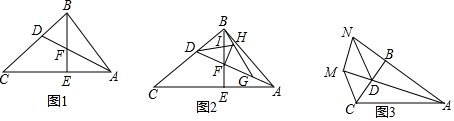
分析 (1)首先证明BD=BF,在Rt△在Rt△ABD中,根据AB=$\sqrt{A{D}^{2}-B{D}^{2}}$计算即可.
(2)如图2中,作BK∥DG交DH的延长线于K,连接KG.首先证明四边形BFGK是平行四边形,再证明IF是△DKG的中位线,由此即可证明.
(3)如图3中,作MK⊥AC于K,MF⊥BC于K,ME⊥AN于E.首先证明△MFD≌△MEN,推出MN=MD,推出∠MDN=45°,由∠BDA=75°,推出∠NDB=180°-45°-75°=60°,设BD=a.则DN=2a,在AB上取一点P,使得PD=PA,则∠DPB=30°,PD=PA=2a,BP=$\sqrt{3}$a,可得AB=(2+$\sqrt{3}$)a,由此即可解决问题.
解答 (1)解:如图1中,
∵BE⊥AC,
∴∠BEC=∠ABC=90°,
∴∠C+∠CBE=90°,∠ABE+∠CBE=90°,
∴∠C=∠ABE,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∵∠BDF=∠C+∠DAC,∠BFD=∠DAB+∠ABE,
∴BD=BF=2$\sqrt{3}$,
在Rt△ABD中,AB=$\sqrt{A{D}^{2}-B{D}^{2}}$=$\sqrt{{6}^{2}-(2\sqrt{3})^{2}}$=2$\sqrt{6}$.
(2)证明:如图2中,作BK∥DG交DH的延长线于K,连接KG.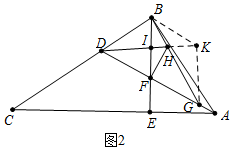
∵FH垂直平分DG,
∴HD=HG,
∴∠HDG=∠HGD,
∴∠HBK=∠HGD,∠HKB=∠HDG,
∴∠HBK=∠HKB,
∴BH=HK,∵∠DHB=∠KHG,
∴△BDH≌△KGH,
∴BD=KG,∵DG=GD,DK=BG,
∴△BDG≌△KGD,
∴∠BDG=∠KGD,
∵∠BDF=∠BFD,
∴∠BFD=∠KGD,
∴BF∥KG,∵BK∥FG,'
∴四边形BFGK是平行四边形,
∴BF=GK=BD,
∵DF=FG,FI∥GK,
∴DI=IK,
∴GK=2IF,
∴BD=2IF.
(3)解:结论:∴$\frac{AB}{DN}$=$\frac{2+\sqrt{3}}{2}$.理由如下,
如图3中,作MK⊥AC于K,MF⊥BC于K,ME⊥AN于E.
∵∠MAE=∠MAK,
∴ME=MK,
∵∠MCK=∠MCB=60°,
∴MK=MF,
∴ME=MF,
∴∠MBE=∠MBF=45°,
∵∠NMD=∠EEMF=90°,
∴∠NME=∠DMF,∵∠MFD=∠MEN,ME=MF,
∴△MFD≌△MEN,
∴MN=MD,
∴∠MDN=45°,
∵∠BDA=75°,
∴∠NDB=180°-45°-75°=60°,设BD=a.则DN=2a,
在AB上取一点P,使得PD=PA,则∠DPB=30°,PD=PA=2a,BP=$\sqrt{3}$a,
∴AB=(2+$\sqrt{3}$)a,
∴$\frac{AB}{DN}$=$\frac{(2+\sqrt{3})a}{2a}$=$\frac{2+\sqrt{3}}{2}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、平行四边形的判定和性质、等腰直角三角形的判定和性质,直角三角形30度角性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,学会用转化的首先思考问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 一户居民一个月用水量即为x米3 | 水费单价 (单位:元/米3) |
| x≤22 | a |
| 超出22米3的部分 | a+1.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为4或6 厘米/秒.
如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为4或6 厘米/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
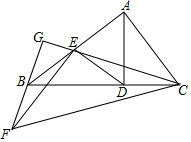 如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.
如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com