
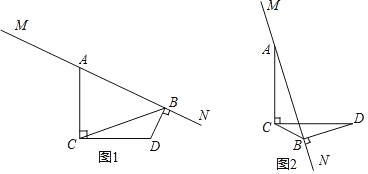
【题目】已知AC=DC,AC⊥DC,直线MN经过点A,作DB⊥MN,垂足为B,连接CB.
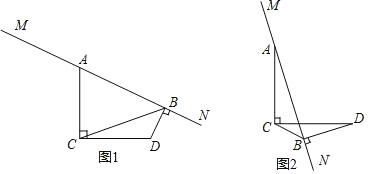
(1)直接写出∠D与∠MAC之间的数量关系;
(2)①如图1,猜想AB,BD与BC之间的数量关系,并说明理由;
②如图2,直接写出AB,BD与BC之间的数量关系;
(3)在MN绕点A旋转的过程中,当∠BCD=30°,BD=![]() 时,直接写出BC的值.
时,直接写出BC的值.
【答案】(1)相等或互补;(2)①BD+AB=![]() BC;②AB﹣BD=
BC;②AB﹣BD=![]() BC;(3)BC=
BC;(3)BC=![]() 或
或![]() .
.
【解析】
(1)分为点C,D在直线MN同侧和点C,D在直线MN两侧,两种情况讨论即可解题,
(2)①作辅助线,证明△BCD≌△FCA,得BC=FC,∠BCD=∠FCA,∠FCB=90°,即△BFC是等腰直角三角形,即可解题, ②在射线AM上截取AF=BD,连接CF,证明△BCD≌△FCA,得△BFC是等腰直角三角形,即可解题,
(3)分为当点C,D在直线MN同侧,当点C,D在直线MN两侧,两种情况解题即可,见详解.
解:(1)相等或互补;
理由:当点C,D在直线MN同侧时,如图1,
∵AC⊥CD,BD⊥MN,
∴∠ACD=∠BDC=90°,
在四边形ABDC中,∠BAD+∠D=360°﹣∠ACD﹣∠BDC=180°,
∵∠BAC+∠CAM=180°,
∴∠CAM=∠D;
当点C,D在直线MN两侧时,如图2,
∵∠ACD=∠ABD=90°,∠AEC=∠BED,
∴∠CAB=∠D,
∵∠CAB+∠CAM=180°,
∴∠CAM+∠D=180°,
即:∠D与∠MAC之间的数量是相等或互补;
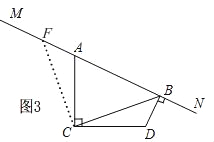
(2)①猜想:BD+AB=![]() BC
BC
如图3,在射线AM上截取AF=BD,连接CF.
又∵∠D=∠FAC,CD=AC
∴△BCD≌△FCA,
∴BC=FC,∠BCD=∠FCA
∵AC⊥CD
∴∠ACD=90°
即∠ACB+∠BCD=90°
∴∠ACB+∠FCA=90°
即∠FCB=90°
∴BF=![]()
∵AF+AB=BF=![]()
∴BD+AB=![]() ;
;
②如图2,在射线AM上截取AF=BD,连接CF,
又∵∠D=∠FAC,CD=AC
∴△BCD≌△FCA,
∴BC=FC,∠BCD=∠FCA
∵AC⊥CD
∴∠ACD=90°
即∠ACB+∠BCD=90°
∴∠ACB+∠FCA=90°
即∠FCB=90°
∴BF=![]()
∵AB﹣AF=BF=![]()
∴AB﹣BD=![]() ;
;

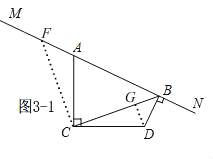
(3)①当点C,D在直线MN同侧时,如图3﹣1,
由(2)①知,△ACF≌△DCB,
∴CF=BC,∠ACF=∠ACD=90°,
∴∠ABC=45°,
∵∠ABD=90°,
∴∠CBD=45°,
过点D作DG⊥BC于G,
在Rt△BDG中,∠CBD=45°,BD=![]() ,
,
∴DG=BG=1,
在Rt△CGD中,∠BCD=30°,
∴CG=![]() DG=
DG=![]() ,
,
∴BC=CG+BG=![]() +1,
+1,
②当点C,D在直线MN两侧时,如图2﹣1,
过点D作DG⊥CB交CB的延长线于G,
同①的方法得,BG=1,CG=![]() ,
,
∴BC=CG﹣BG=![]() ﹣1
﹣1
即:BC=![]() 或
或![]() ,
,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
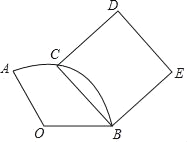
【题目】如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在![]() 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
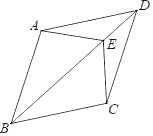
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果∠BDC=30°,DE=2,EC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )

A. ![]() B.
B. ![]() C. 2﹣
C. 2﹣ ![]() D. 1+
D. 1+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿对角线BD折叠,使点C落
在E处,BE与AD相交于F,下列结论:①BD2=AD2+AB2
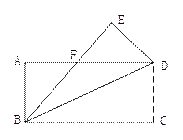 ②△ABF≌△EDF ③
②△ABF≌△EDF ③![]() ④AD=BD·cos45°正确的是( )
④AD=BD·cos45°正确的是( )
A. ①② B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+ c(a≠0).
(1)若抛物线与x轴交于点B(4,0),且过点P(1,–3),求该抛物线的解析式;
(2)若a>0,c =0,OA、OB是过抛物线顶点的两条互相垂直的直线,与抛物线分别交于A、B 两点,求证:直线AB恒经过定点(0,![]() );
);
(3)若a>0,c <0,抛物线与x轴交于A,B两点(A在B左边),顶点为C,点P在抛物线上且位于第四象限.直线PA、PB与y轴分别交于M、N两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
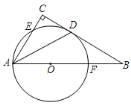
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com