
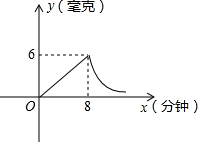
 为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题:
为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题:分析 (1)从药物释放开始,设函数解析式为y=kx,设药物释放完毕后,y与x函数关系式y=$\frac{a}{x}$,分别把(8,6)代入可分别计算出k、a的值,进而可得函数解析式;
(2)根据y<1.6,结合反比例函数解析式可得$\frac{48}{x}$<1.6,再解不等式即可;
(3)根据题意可得不等式组$\left\{\begin{array}{l}{\frac{3}{4}x≥3}\\{\frac{48}{x}≥3}\end{array}\right.$,计算出不等式组的解集,然后可得答案.
解答 解:(1)从药物释放开始,设函数解析式为y=kx,
∵经过(8,6),
∴6=8k,
解得:k=$\frac{3}{4}$,
∴y=$\frac{3}{4}$x(x≤8);
设药物释放完毕后,y与x函数关系式y=$\frac{a}{x}$,
∵经过(8,6),
∴a=48,
∴y=$\frac{48}{x}$;
故答案为:y=$\frac{3}{4}$x;x≤8;y=$\frac{48}{x}$;
(2)当y<1.6时,$\frac{48}{x}$<1.6,
解得:x>30;
(3)当y≥3时,$\left\{\begin{array}{l}{\frac{3}{4}x≥3}\\{\frac{48}{x}≥3}\end{array}\right.$,
解得:4≤x≤16,
∵16-4=12>10,
∴此次消毒是有效.
点评 此题主要考查了反比例函数的应用,关键是正确理解题意,掌握待定系数法求反比例函数解析式的方法.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{b}{a}$+$\frac{2}{b}$=$\frac{b+2}{a+b}$ | B. | ($\frac{-y}{2x}$)2=$\frac{{y}^{2}}{2x}$ | C. | y2÷y-3=y-1 | D. | $\frac{a}{a-b}$-$\frac{b}{a-b}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.
如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com