
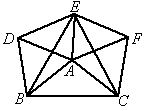
如图所示,以△ABC的三边在BC边的同侧分别作三个等边三角形△ABD、△BCE、△ACF,试问△ABC满足什么条件时,四边形ADEF为矩形?
|
解: 当∠BAC=150°时,四边形ADEF是矩形在△ DBE和△ABC中,DB=AB,EB=CB∠ DBE=∠DBA-∠EBA=60°-∠EBA=∠EBC-∠EBA=∠ABC所以△ DBE与△ABC全等∴ DE=AC=AF同理 DA=BA=EF,所以四边形ADEF为平行四边形所以∠ DAF=90°时□ADEF为矩形因为△ ABD和△ACF都是等边三角形所以∠ BAD=∠CAF=60°∠ BAC=360°-(∠BAD+∠CAF+∠DAF)=150°因此当∠ BAC=150°时,四边形ADEF是矩形. |
|
先识别四边形 ADEF为平行四边形,要使它为矩形,就只要∠DAF=90°即可.因为∠DAB=∠FAC=60°,所以通过计算出∠BAC的大小,就得△ABC应满足的条件 |


科目:初中数学 来源: 题型:
 30、如图所示,以△ABC的三边为边,分别作三个等边三角形.
30、如图所示,以△ABC的三边为边,分别作三个等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 29、如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF是什么四边形,试证明你的结论.
29、如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF是什么四边形,试证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:
 24、已知:如图所示,以△ABC的三边为边,在BC的同侧分别作等边△ABD、△BCE、△ACF.
24、已知:如图所示,以△ABC的三边为边,在BC的同侧分别作等边△ABD、△BCE、△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:
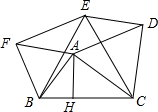 如图所示,以△ABC的三边为边在BC的同侧作正三角形BCE,正三角形ABF和正三角形ACD,已知BC=3,高AH=1,则五边形BCDEF的面积是
如图所示,以△ABC的三边为边在BC的同侧作正三角形BCE,正三角形ABF和正三角形ACD,已知BC=3,高AH=1,则五边形BCDEF的面积是查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com