
【题目】如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数![]() (x>0)和
(x>0)和![]() (x>0)的图象于点P和Q,连接OP、OQ,则下列结论正确的是( )
(x>0)的图象于点P和Q,连接OP、OQ,则下列结论正确的是( )

A. ∠POQ不可能等于900 B. ![]()
C. 这两个函数的图象一定关于x轴对称 D. △POQ的面积是![]()
【答案】D
【解析】试题分析:根据反比例函数的性质,xy=k,以及△POQ的面积=![]() MOPQ分别进行判断即可得出答案.
MOPQ分别进行判断即可得出答案.
解:A.∵P点坐标不知道,当PM=MQ时,并且PM=OM,∠POQ等于90°,故此选项错误;
B.根据图形可得:k1>0,k2<0,而PM,QM为线段一定为正值,故PM:QM=|k1|:|k2|,故此选项错误;
C.根据k1,k2的值不确定,得出这两个函数的图象不一定关于x轴对称,故此选项错误;
D.∵|k1|=PMMO,|k2|=MQMO,△POQ的面积=![]() MOPQ=
MOPQ=![]() MO(PM+MQ)=
MO(PM+MQ)=![]() MOPM+
MOPM+![]() MOMQ,
MOMQ,
∴△POQ的面积是![]() (|k1|+|k2|),故此选项正确.
(|k1|+|k2|),故此选项正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】一家化工厂原来每月利润为120万元,从今年1月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平.
(1)设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y,写出y关于x的函数关系式,并求前几个月的利润和等于700万元;
(2)当x为何值时,使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等;
(3)求使用回收净化设备后两年的利润总和.
查看答案和解析>>
科目:初中数学 来源: 题型:
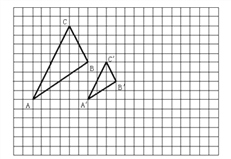
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B'C'的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点 O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com