
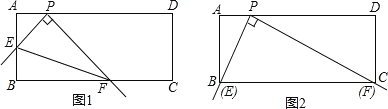
【题目】在矩形ABCD中,点P在AD上,AB=![]() ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).当点E与点B重合时,点F恰好与点C重合(如图2).将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径长为.
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).当点E与点B重合时,点F恰好与点C重合(如图2).将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径长为.
【答案】![]()
【解析】
根据题意先利用相似三角形的判定与性质求得图2中PC的长,再设线段EF的中点为O,连接OP,OB,如图1,证明得到O点在线段BP的垂直平分线上,然后如图2,当点E与点B重合时,点F与点C重合时,EF的中点为BC的中点O,当点E与点,A重合时,EF的中点为PB的中点O,得到OO′为△PBC的中位线,即OO′=![]() PC.
PC.
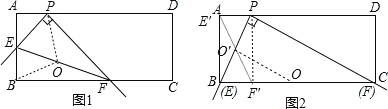
解:如图2,
在矩形ABCD中,∠A=∠D=90°,
∵AP=1,AB=![]() ,
,
∴PB=![]() =2,
=2,
∵∠ABP+∠APB=90°,∠BPC=90°,
∴∠APB+∠DPC=90°,
∴∠ABP=∠DPC,
∴△APB∽△DCP,
∴AP:CD=PB:CP,即1:![]() =2:PC,
=2:PC,
∴PC=2![]() ,
,
设线段EF的中点为O,连接OP,OB,如图1,
在Rt△EPF中,OP=![]() EF,
EF,
在Rt△EBF中,OB=![]() EF,
EF,
∴OP=OB,
∴O点在线段BP的垂直平分线上,
如图2,当点E与点B重合时,点F与点C重合时,EF的中点为BC的中点O,
当点E与点,A重合时,EF的中点为PB的中点O,
∴OO′为△PBC的中位线,
∴OO′=![]() PC=
PC=![]() ,
,
∴线段EF的中点经过的路线长为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
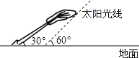
【题目】如图,太阳光线与地面成![]() 角,一棵倾斜的大树与地面成
角,一棵倾斜的大树与地面成![]() 角,这时测得大树在地面上的影长约为
角,这时测得大树在地面上的影长约为![]() ,则大树的长约为________
,则大树的长约为________![]() (保留两个有效数字,下列数据供选用:
(保留两个有效数字,下列数据供选用:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
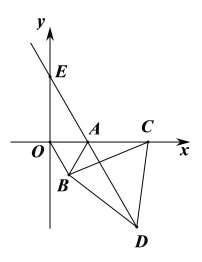
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以线段
,以线段![]() 为边在第四象限内作等边三角形
为边在第四象限内作等边三角形![]() ,点
,点![]() 为
为![]() 正半轴上一动点
正半轴上一动点![]() , 连接
, 连接![]() ,以线段
,以线段![]() 为边在第四象限内作等边三角形
为边在第四象限内作等边三角形![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 轴于点
轴于点![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的度数是否会变化?如果不变,请求出
的度数是否会变化?如果不变,请求出![]() 的度数;如果变化,请说明理由.
的度数;如果变化,请说明理由.
(3)当点![]() 运动到什么位置时,以
运动到什么位置时,以![]() 为顶点的三角形是等腰三角形?
为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() ,把一条长为2016个单位长度且没有弹性的细线
,把一条长为2016个单位长度且没有弹性的细线![]() 线的粗细忽略不计
线的粗细忽略不计![]() 的一端固定在点A处,并按
的一端固定在点A处,并按![]() 的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是![]()
![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一条直线上,连结BD,BE.以下四个结论:①BD=CE ;②BD⊥CE ;③∠ACE+∠DBC=45°; ④∠ACE=∠DBC ,其中结论正确的是____________
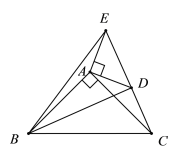
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在R△ABC中,∠ACB=90°,AC=6,BC=8,E为AC上一点,且AE=![]() ,AD平分∠BAC交BC于D.若P是AD上的动点,则PC+PE的最小值等于( )
,AD平分∠BAC交BC于D.若P是AD上的动点,则PC+PE的最小值等于( )
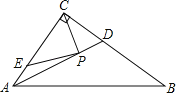
A.![]() B.
B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
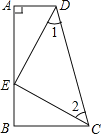
(1)求证:△ADE≌△BEC;
(2)若AD=3,AB=9,求△ECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为4m的正方形,使不规则区域落在正方形内.现向正方形内随机投掷小球(假设小球落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小球落在不规则区域的频率稳定在常数0.65附近,由此可估计不规则区域的面积约为( )

A. 2.6m2 B. 5.6m2 C. 8.25m2 D. 10.4m2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com