
【题目】如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.
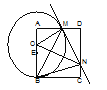
求证:(1)△AOM∽△DMN; (2)求∠MBN的度数.
【答案】(1)、证明过程见解析;(2)、45°.
【解析】试题分析:(1)、根据切成的性质得出∠AMO+∠DMN=90°,根据正方形性质得出∠A=∠D=90°,即∠AMO+∠AOM=90°,从而得出∠AOM=∠DMN,得出三角形相似;(2)、作BP⊥MN,根据切线和AD∥BC得出Rt△MAB≌Rt△MPB,得到∠ABM=∠MBP,BP=AB=BC,然后得出Rt△BPN≌Rt△BCN,得出∠PBN=∠CBN,根据∠MBN=∠MBP+∠PBN=![]() ∠ABC得出答案.
∠ABC得出答案.
试题解析:(1)、∵MN是⊙O的切线, ∴OM⊥MN,∴∠AMO+∠DMN=90°,
又∵四边形ABCD为正方形, ∴∠A=∠D=90°,∴∠AMO+∠AOM=90°, ∴∠AOM=∠DMN,
∴△AMO∽△DMN
(2)、如图,作BP⊥MN于点P,

∵MN是⊙O的切线,∴∠PMB+∠BMO=90°,
∵∠ABC=90°,∴∠CBM+∠MBO=90°, ∵OB=OM,∴∠BMO=∠MBO, ∴∠PMB=∠CBM,
∵AD∥BC,∴∠CBM=∠AMB, ∴∠AMB=∠PMB,
在Rt△MAB和Rt△MPB中, , ∴Rt△MAB≌Rt△MPB(AAS)
, ∴Rt△MAB≌Rt△MPB(AAS)
∴∠ABM=∠MBP,BP=AB=BC,
在Rt△BPN和Rt△BCN中,![]() , ∴Rt△BPN≌Rt△BCN(HL) ∴∠PBN=∠CBN,
, ∴Rt△BPN≌Rt△BCN(HL) ∴∠PBN=∠CBN,
∴∠MBN=∠MBP+∠PBN=![]() ∠ABC=45°.
∠ABC=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
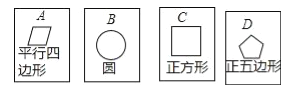
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市辖区内长江流域水质情况的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对重庆电视台“天天630”栏目收视率的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
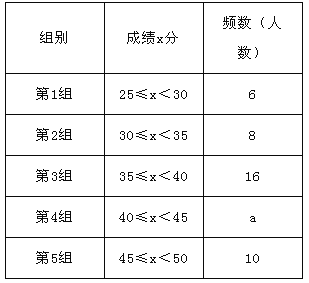
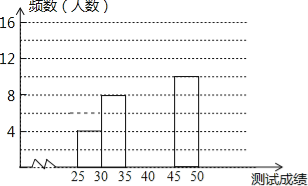
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列关于自然数的等式:
(i)32﹣4×12=5 ①
(ii)52﹣4×22=9 ②
(iii)72﹣4×32=13 ③
…
根据上述规律解决下列问题:
(1)完成第五个等式:112﹣4× 2=;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
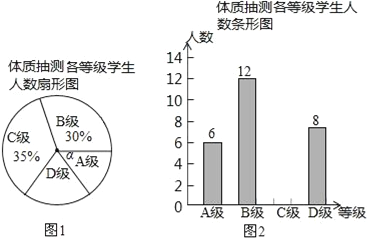
【题目】为了进一步了解义务教育阶段学生的体质健康状况,某县从全县九年级学生中随机抽取了部分学生进行了体质抽测.体质抽测的结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格.并根据抽测结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)本次抽测的学生人数是 人;
(2)图(1)中∠α的度数是 ,并把图(2)条形统计图补充完整;
(3)该县九年级有学生4800名,如果全部参加这次体质测试,请估计不合格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中H为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com