
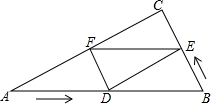
 如图,△ABC中,∠C=90°,BC=5,AC=5$\sqrt{3}$,点D从A出发沿AB以每秒2个单位的速度向点B匀速运动,同时,点E从B出发沿BC以每秒1个单位的速度向点C匀速运动.当一个点到达终点时,另一个点也停止运动.设点D、E运动的时间为t(t>0),作DF⊥AC于F,连DE、EF.
如图,△ABC中,∠C=90°,BC=5,AC=5$\sqrt{3}$,点D从A出发沿AB以每秒2个单位的速度向点B匀速运动,同时,点E从B出发沿BC以每秒1个单位的速度向点C匀速运动.当一个点到达终点时,另一个点也停止运动.设点D、E运动的时间为t(t>0),作DF⊥AC于F,连DE、EF.分析 (1)先根据动点的速度、时间表示路程:AD=2t,EB=t,再根据三角函数值求∠A=30°,则DF=t,可得结论;
(2)先根据一组对边平行且相等的四边形是平行四边形证明四边形BEFG为平行四边形,若使?AEFD为菱形则需要满足的条件:DF=BD,列方程可求得结论;
(3)①∠EDF=90°时,证明四边形ECFD为矩形,根据DF=CE列式求得;
②∠DEF=90°时,由(2)知EF∥AD,则得∠ADE=∠DEF=90°,根据BE=2BD列式求得;
③∠EFD=90°时,此种情况不存在.
解答 (1)证明:如图1,由题意得:AD=2t,EB=t,
在Rt△ACB中,tan∠A=$\frac{BC}{AC}=\frac{5}{5\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∴DF=$\frac{1}{2}$AD=t,
又∵EB=t,
∴EB=DF;
(2)解:如图2,∵AC⊥BC,DF⊥AC,
∴BC∥DF,
又EB=DF,
∴四边形BEFD为平行四边形,
在Rt△ABC中,∠A=30°,BC=5,
∴AB=2BC=10,
∴BD=AB-AD=10-2t,
若使?BEFD为菱形,则需DF=BD,
即t=10-2t,t=$\frac{10}{3}$,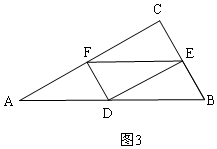
即当t=$\frac{10}{3}$时,四边形BEFD为菱形;
(3)解:△DEF为直角三角形时,要分三种情况:
①如图3,当∠EDF=90°时,
∴∠EDF=∠C=∠DFC=90°,
∴四边形ECFD为矩形,
∴DF=CE,
即t=5-t,t=$\frac{5}{2}$;
②如图4,∠DEF=90°时,
由(2)四边形EFDB为平行四边形,
∴EF∥AD,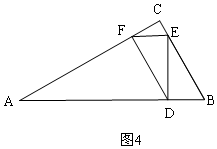
∴∠BDE=∠DEF=90°,
∴∠B=90°-∠A=60°,
∴∠DEB=90°-60°=30°,
∴BE=2BD,
即t=2(10-2t),t=4,
③∠EFD=90°时,此种情况不存在;
综上所述,当t=$\frac{5}{2}$秒或4秒时,△DEF为直角三角形.
故答案为:t=$\frac{5}{2}$秒或4秒.
点评 本题是四边形的综合题,考查了动点运动问题、菱形的性质和判定、平行四边形、矩形的性质和判定、三角函数问题,难度适宜,根据不同结论确定其等量关系,列方程可以解决问题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
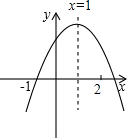 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.
已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com