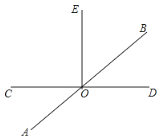
【题目】如图，已知直线AB和CD相交于点O，在∠COB的内部作射线OE.
（1）若∠AOC=36°，∠COE=90°，求∠BOE的度数；
（2）若∠COE：∠EOB：∠BOD=4：3：2，求∠AOE的度数.
【答案】解：（1）54°；（2）120°
【解析】试题分析：（1）由对顶角相等可得∠AOC=∠BOD=36°，由∠COE=90°可得∠EOD=90°，所以∠BOE=∠EOD－∠BOD=54°；（2）由∠COE：∠EOB：∠BOD=4：3：2，可得∠EOB=180°×
=60°，所以∠AOE=180°－∠EOB=120°.
试题解析：
解：（1）∵∠AOC=36°，∠COE=90°，
∴∠BOD=36°，∠EOD=90°，
∴∠BOE=90－36°=54°；
（2）∠COE：∠EOB：∠BOD=4：3：2，
∴∠EOB=180°×
=60°，
∴∠AOE=180°－∠EOB=180°－60°=120°.
科目：初中数学 来源： 题型：
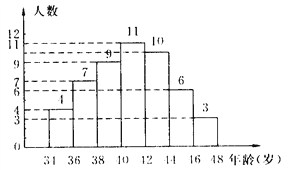
【题目】如图是某单位职工的年龄（取正整数）的频率分布直方图，根据图中提供的信息，回答下列问题：
（1）该单位共有职工多少人？
（2）不小于38岁但小于44岁的职工人数占职工总人数的百分比是多少？
（3）如果42岁的职工有4人，那么年龄在42岁以上的职工有几人？
查看答案和解析>>
科目：初中数学 来源： 题型：
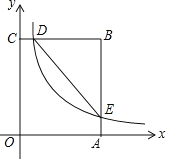
【题目】如图，在矩形OABC中，OA＝3，OC＝5，分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y＝
（k＞0）的图象经过点D且与边BA交于点E，连接DE．
（1）连接OE，若△EOA的面积为3，则k＝___________；
（2）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
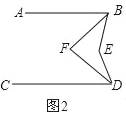
【题目】将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和为（ ）
A．2cm2 B．4cm2 C．6cm2 D．8cm2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，，点D是边AB上一点，E为AC的中点，过点C作CF∥AB， 交DE的延长线于点F。
（1）求证：DE=FE；
（2）若CD=CF，∠A=40°，求∠BCD的度数。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
（1）当直线MN绕点C旋转到图1的位置时，求证：DE=AD+BE；
（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，直线AB∥CD
（1）如图1，点E在直线BD的左侧，猜想∠ABE、∠CDE、∠BED的数量关系，并证明你的结论；
（2）如图2，点E在直线BD的左侧，BF、DF分别平分∠ABE、∠CDE，猜想∠BFD和∠BED的数量关系，并证明你的结论；
（3）如图3，点E在直线BD的右侧，BF、DF分别平分∠ABE、∠CDE；那么第（2）题中∠BFD和∠BED的数量关系的猜想是否仍成立？如果成立，请证明；如果不成立，请写出你的猜想，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D，已知AC＝3，BC＝4.
(1)线段AD，CD，CD，BD是不是成比例线段？写出你的理由；
(2)在这个图形中，能否再找出其他成比例的四条线段？如果能，请至少写出两组．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com