
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

【答案】(1)8;(2)80°.
【解析】
根据多边形的外角和为360°,内角和公式为:(n-2)180°,由题意可知:内角和=3×外角和,设出未知数,可得到方程,解方程即可.
在直角三角形DFB中,根据三角形内角和定理,求得∠B的度数;再在△ABC中,根据内角与外角的性质求∠ACF的度数即可.
(1)设这个多边形的边数为n,
∵n边形的内角和为(n﹣2)180°,多边形的外角和为360°,
∴(n﹣2)180°=360°×3,
解得n=8.
∴这个多边形的边数为8.
(2)在△DFB中,
∵DF⊥AB,
∴∠FDB=90°,
∵∠F=40°,∠FDB+∠F+∠B=180°,
∴∠B=50°.
在△ABC中,
∵∠A=30°,∠B=50°,
∴∠ACF=30°+50°=80°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,∠COD=90°,OE、OF分别是∠COB、∠AOD的平分线,且∠COB:∠AOD=4:9.
(1)写出图中∠BOD的余角和补角;
(2)求∠AOC的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,CD垂直AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F.
(1)若P为BC边中点,则PE,PF,CD三条线段有何数量关系(写出推理过程)?
(2)若P为线段BC上任意一点,则(1)中关系还成立吗?
(3)若P为直线BC上任意一点,则PE,PF,CD三条线段间有何数量关系(请直接写出).
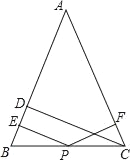
查看答案和解析>>
科目:初中数学 来源: 题型:
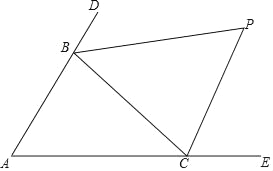
【题目】如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.

供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好. 
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E
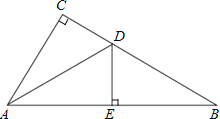
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若∠2=∠6,则____∥___;如果∠BCD+∠ADC=180°,那么____∥____;如果∠9=_____,那么AD∥BC;如果∠9=____,那么AB∥CD;
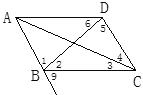
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,一组互相平行的直线共有n条(n≥2,且n为正整数),它们和两条平行线a,b相交,构成若干个“#”字形. 设构成的“#”字形的个数为x,请找出规律,并填写下表.

n | 2 | 3 | 4 | 5 | … | n |
x | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com