
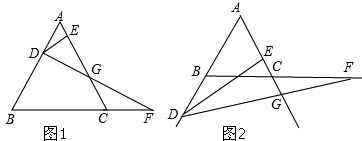
���� ��1����AD=x����BD=4-x��BF=4+x����DF��ABʱ��ͨ����ֱ�ǡ�BDF���x��ֵ����t��ֵ��
��2����ͼ1������D��DH��BC��AC�ڵ�H������ȫ�������Σ���DHG�ա�FCG�����ȫ�������εĶ�Ӧ����ȵ����ʺ�ͼ������߶μ�ĺͲ��ϵ���DG=GF��
��3����F��FH��AC����֤��ADE�ա�CFH����DE=FH��AC=EH����֤��GDE�ա�GFH���ɵ�EG=GH�����ɽ��⣮
��� 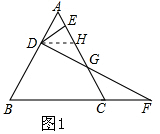 �⣺��1����AD=x����BD=4-x��BF=4+x��
�⣺��1����AD=x����BD=4-x��BF=4+x��
��DF��ABʱ���ߡ�B=60�㣬
���DFB=30�㣬
��BF=2BD����4+x=2��4-x����
���x=$\frac{4}{3}$��
��t=$\frac{4}{3}$
��2����ͼ1������D��DH��BC��AC�ڵ�H�����DHG=��FCG��
�ߡ�ABC�ǵȱ������Σ�
���ADH�ǵȱ������Σ�
��AD=DH��
��AD=CF��
��DH=FC��
���ڡ�DHG���FCG�У�$\left\{\begin{array}{l}{��DGH=��FGC}\\{��DHG=��FCG}\\{DH=FC}\end{array}\right.$��
���DHG�ա�FCG��AAS����
��DG=GF��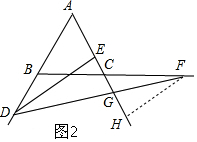
��3����F��FH��AC��
�ڡ�ADE�͡�CFH�У�
$\left\{\begin{array}{l}{��AED=��FHC=90��}\\{��A=��FCH}\\{AD=CF}\end{array}\right.$��
���ADE�ա�CFH��AAS����
��DE=FH��AE=CH��
��AC=EH��
�ڡ�GDE�͡�GFH�У�
$\left\{\begin{array}{l}{��DEG=��FHG}\\{��DGE=��FGH}\\{DE=FH}\end{array}\right.$��
���GDE�ա�GFH��AAS����
��EG=GH��
��EG=$\frac{1}{2}$EH=$\frac{1}{2}$AC��
���� ���⿼�����������ۺ��⣬��Ҫ����ȫ�������ε��ж���������ȫ�������ζ�Ӧ����ȵ����ʣ���������֤GDE�ա�GFH�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
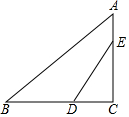 ��ͼ����Rt��ABC�У���C=90�㣬AB=5��AC=3����D��E�ֱ��DZ�BC��AC�ϵĵ㣬�ҡ�EDC=��A������ABC��DE���ۣ�����Cǡ�����ڱ�AB�ϣ��� DE�ij�Ϊ$\frac{125}{48}$��
��ͼ����Rt��ABC�У���C=90�㣬AB=5��AC=3����D��E�ֱ��DZ�BC��AC�ϵĵ㣬�ҡ�EDC=��A������ABC��DE���ۣ�����Cǡ�����ڱ�AB�ϣ��� DE�ij�Ϊ$\frac{125}{48}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
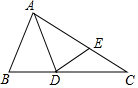 ��ͼ����ABC�У���B=2��C��������AD�۵���ʹ��B���ڱ�AC�ϵĵ�E������ͼ����BD��ȵ������߶ηֱ���EC��DE��
��ͼ����ABC�У���B=2��C��������AD�۵���ʹ��B���ڱ�AC�ϵĵ�E������ͼ����BD��ȵ������߶ηֱ���EC��DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
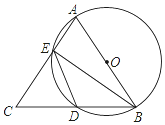 ��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ������O����O�ֱ�AC��BC�ڵ�E��D������ED��BE��
��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ������O����O�ֱ�AC��BC�ڵ�E��D������ED��BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
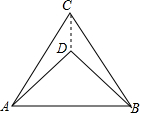 ��ͼ����һ�ŵ���ֱ��������ֽƬABD��һ�ŵȱ�������ֽƬABC����һ�𣨵���ֱ�������ε�б�ߵ��ڵȱ������εı߳�����AB=2$\sqrt{3}$����CD=3-$\sqrt{3}$��
��ͼ����һ�ŵ���ֱ��������ֽƬABD��һ�ŵȱ�������ֽƬABC����һ�𣨵���ֱ�������ε�б�ߵ��ڵȱ������εı߳�����AB=2$\sqrt{3}$����CD=3-$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com