
 )时,四边形AOCP的面积达到最大值
)时,四边形AOCP的面积达到最大值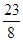
 OC=
OC= (m-1) ∴点B的坐标为(
(m-1) ∴点B的坐标为( ) (4分)
) (4分)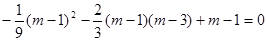
 ∴m=4 (7分)
∴m=4 (7分)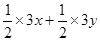 (10分)=
(10分)= (12分)
(12分) )时,四边形AOCP的面积达到最大值
)时,四边形AOCP的面积达到最大值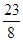 (14分)
(14分)

科目:初中数学 来源:不详 题型:单选题
 烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度
烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度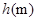 与飞行时间
与飞行时间 的关系式是
的关系式是 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )A.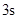 | B.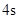 | C.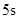 | D.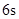 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
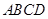 的顶点
的顶点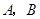 的坐标分别为
的坐标分别为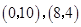 ,顶点
,顶点 在第一象限.点
在第一象限.点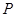 从点
从点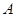 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点 从点
从点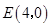 出发,沿
出发,沿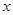 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点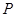 到达点
到达点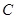 时,
时,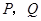 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为 秒.
秒.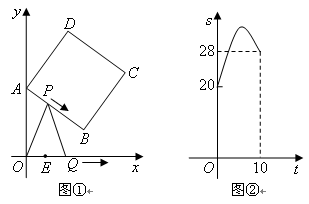
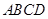 的边长.(2分)
的边长.(2分)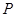 在
在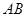 边上运动时,
边上运动时, 的面积
的面积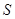 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求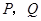 两点的运动速度.(2分)
两点的运动速度.(2分)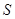 (平方单位)与时间
(平方单位)与时间 (秒)的函数关系式及面积
(秒)的函数关系式及面积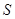 取最大值时点
取最大值时点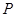 的坐标.(4分)
的坐标.(4分)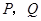 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点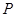 沿着
沿着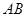 边运动时,
边运动时,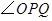 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时,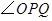 的大小随着时间
的大小随着时间 的增大而减小.当点
的增大而减小.当点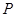 沿着这两边运动时,使
沿着这两边运动时,使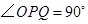 的点
的点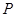 有 个.(2分)
有 个.(2分)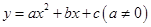 的顶点坐标是
的顶点坐标是 .)
.)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
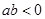 ;②方程
;②方程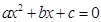 的根为
的根为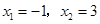 ;
; ;④当
;④当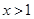 时,y随x值的增大而增大;
时,y随x值的增大而增大; 时,
时,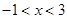 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.2个 | B.3个 | C.4个 | D.5个 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com