
(11·佛山)阅读材料
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;
比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明;
解:(1)
性质1:只有一组对角相等(或者∠B=∠D,∠A≠∠C); …………………………1分
性质2:只有一条对角线平分对角; ……………………………………………………2分
性质有如下参考选项:
性质3:两条对角线互相垂直,其中只有一条被另一条平分;
性质4:两组对边都不平行.
(2)判定方法1:只有一条对角线平分对角的四边形是筝形;…………………………4分
判定方法2:两条对角线互相垂直且只有一条被平分的四边形是筝形;…………………6分
判定方法有如下参考选项:
判定方法3:AC⊥BD,∠B=∠D,∠A≠∠C;
判定方法4:AB=CD,∠B=∠D,∠A≠∠C;
判定方法5:AC⊥BD,AB=CD,∠A≠∠C.
判定方法1的证明:
已知:在四边形ABCD中,对角线AC平分∠A和∠C,对角线BD不平分∠B和∠D.
求证:四边形ABCD是筝形.
证明:∵∠BAC=∠DAC,∠BCA=∠DCA,AC=AC,∴△ABC≌△ADC.
∴AB=CD,CB=CD,①…………………………………………………………………8分
易知AC⊥BD.
又∵∠ABD≠∠CBD,
∴∠BAC≠∠BCA,∴AB≠BC.②……………………………………………………10分
由①、②知四边形ABCD是筝形.……………………………………………………11分
判定方法2的证明:
AC⊥BD,(不妨)BE=DE→AB=CD,CB=CD.AE≠CE→AB≠BC.
判定方法3的证明:
若B、D不是关于AC对称,则有∠ABD<∠ADB,∠CBD<∠CDB(或反之)→与∠B=∠D矛盾→B、D关于AC对称→AB=CD,CB=CD. ∠A≠∠CAE→∠BAC≠∠BCA→AB≠BC.
判定方法4的证明:
AB=CD→∠ABD=∠ADB(结合∠B=∠D)→∠CBD=∠CDB→CB=CD.
以下同判定方法3.
判定方法5的证明:对照3和4 的证明.
其他判定方法及证明参照给分.
解析:略


科目:初中数学 来源:2011年初中毕业升学考试(广西梧州卷)数学 题型:解答题
(11·佛山)阅读材料
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;
比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明;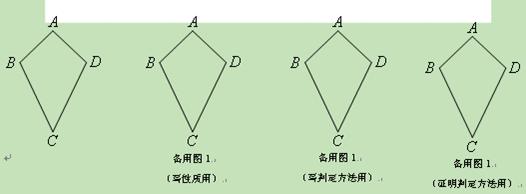
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西梧州卷)数学 题型:解答题
(11·佛山)阅读材料
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;
比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形;
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
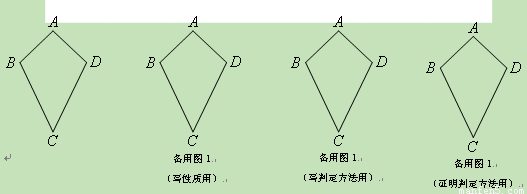
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明;
查看答案和解析>>
科目:初中数学 来源:2010年江苏省盐城市阜宁县实验初中初三数学试卷(解析版) 题型:解答题
 x-2)2+
x-2)2+ x2是x2-2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项--见横线上的部分).
x2是x2-2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项--见横线上的部分).查看答案和解析>>
科目:初中数学 来源:2010年江苏省盐城市阜宁县实验初中九年级一模数学试卷(解析版) 题型:解答题
 x-2)2+
x-2)2+ x2是x2-2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项--见横线上的部分).
x2是x2-2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项--见横线上的部分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com