
【题目】抛物线y=﹣![]() x交x轴于点A,点B(6,n)为抛物线上一点.
x交x轴于点A,点B(6,n)为抛物线上一点.
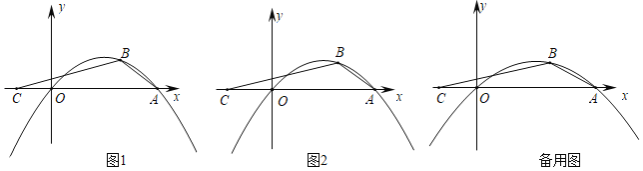
(1)求m与n之间的函数关系;
(2)如图,点C(﹣n,0)在x轴上,且∠BAC=2∠ACB,求m的值;
(3)在(2)的条件下,P为直线BC上方抛物线上一点,过点P作PD∥AB交x轴于点D,DE⊥BC交OP于点E,![]() ,求点P坐标.
,求点P坐标.
【答案】(1)n=m;(2)3;(3)P(4,3)
【解析】
(1)将点B(6,n)代入y=﹣![]() x,得到n=m;
x,得到n=m;
(2)过点B作BG⊥x轴,作∠BAC的角平分线交BG于点M,过点M作MN⊥AB,求出A(![]() n+6,0),B(6,n),在Rt△ABC中,tan∠BAO=
n+6,0),B(6,n),在Rt△ABC中,tan∠BAO=![]() ,可求得tan∠MAG=tan∠BAC=
,可求得tan∠MAG=tan∠BAC=![]() ,则有
,则有![]() =
=![]() ,即可求出n=m=3;
,即可求出n=m=3;
(3)由(2)可得y=﹣![]() x2+
x2+![]() x,设P(t,﹣
x,设P(t,﹣![]() t2+
t2+![]() t),由
t),由![]() 可得
可得![]() =
=![]() ,所以求出E(
,所以求出E(![]() t,﹣
t,﹣![]() t2+2t),分别求出BC的解析式为y=
t2+2t),分别求出BC的解析式为y=![]() x+1,DE的解析式为y=﹣3x﹣
x+1,DE的解析式为y=﹣3x﹣![]() t2+
t2+![]() t,即可求D(﹣
t,即可求D(﹣![]() t2+
t2+![]() t,0),又由DP∥AB,得到
t,0),又由DP∥AB,得到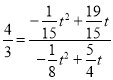 ,所以t=4即可求P的坐标.
,所以t=4即可求P的坐标.
(1)将点B(6,n)代入y=﹣![]() x,得:
x,得:
n=![]() ,
,
化简得:n=m;
(2)过点B作BG⊥x轴,作∠BAC的角平分线交BG于点M,过点M作MN⊥AB,
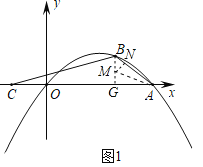
∵A(![]() n+6,0),B(6,n),
n+6,0),B(6,n),
∴AG=![]() n,
n,
在Rt△ABG中,tan∠BAO=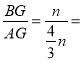
![]() ,
,
∵MN⊥AB,MG⊥OA,
∴MN=MG,
∵在Rt△MNB和Rt△AGB中,∠B为相等的角,
∴Rt△MNB∽Rt△AGB
∴![]() ,
,
设BN=3x,MN=4x,则BM=5x,
∵BG-MB=MG,MG=MN,
∴n-5x=4x,解得x=![]() ,
,
∴MG=MN=![]() ,
,
∴tan∠MAG= ,
,
∵∠BAC=2∠ACB,
∴tan∠BAC=![]() ,
,
∵C(﹣n,0),
∴![]() =
=![]() ,
,
∴n=3,
∴m=3;
(3)如图所示:
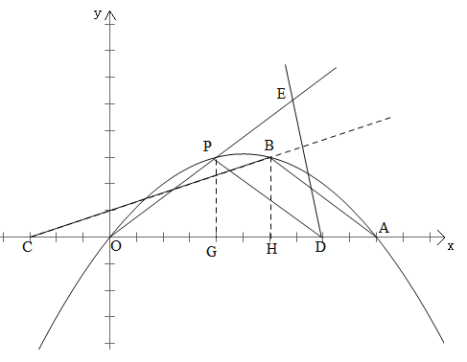
由(2)可得y=﹣![]() x2+
x2+![]() x,
x,
设P(t,﹣![]() t2+
t2+![]() t),
t),
∵![]() ,
,
∴![]() =
=![]() ,
,
∴E(![]() t,﹣
t,﹣![]() t2+2t),
t2+2t),
∵B(6,3),A(10,0),C(﹣3,0),
∴BC的解析式为y=![]() x+1,
x+1,
∵BC⊥DE,
∴设直线DE的解析式为y=-3x+k,
把E(![]() t,﹣
t,﹣![]() t2+2t)代入y=-3x+k中得:k=﹣
t2+2t)代入y=-3x+k中得:k=﹣![]() t2+
t2+![]() t,
t,
∴DE的解析式为y=﹣3x﹣![]() t2+
t2+![]() t,
t,
∴D(﹣![]() t2+
t2+![]() t,0),
t,0),
∵DP∥AB,
∴![]() ,
,
∴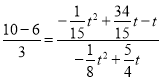 即
即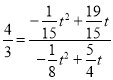 ,
,
∴解方程得:t=4或t=0(增根,舍去),
∵P点在BC直线上方,
∴t>0,
∴t=4符合题意,
∴P(4,3).


科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价
元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,若商场平均每天要盈利
件,若商场平均每天要盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
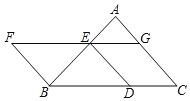
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=30°,![]() 时,求D,F两点间的距离.
时,求D,F两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.
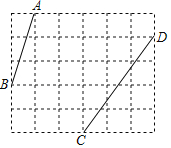
(1)画出一个以AB为一边的△ABE,点E在小正方形的顶点上,且∠BAE=45°,△ABE的面积为![]() ;
;
(2)画出以CD为一腰的等腰△CDF,点F在小正方形的顶点上,且△CDF的面积为![]() ;
;
(3)在(1)、(2)的条件下,连接EF,请直接写出线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
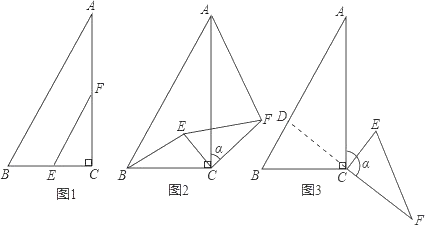
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,![]() = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
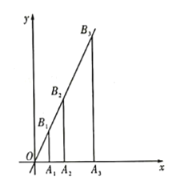
【题目】如图,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ;点
;点![]() 与点
与点![]() 关于直线
关于直线![]() 对称;过点
对称;过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ;点
;点![]() 与点
与点![]() 关于直线
关于直线![]() 对称;过点
对称;过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ;
;![]() ,按此规律作下去,则点
,按此规律作下去,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
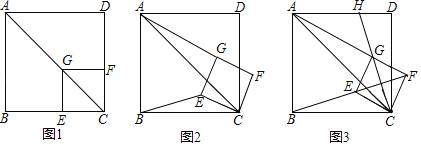
【题目】如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明:四边形CEGF是正方形;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)拓展与运用:
正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=6,GH=2![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com