练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    关于的方程为．

    1.证明：方程有两个不相等的实数根．

    2.是否存在实数m，使方程的两个实数根互为相反数？若存在，求出m的值及两个实数根；若不存在，请说明理由．

     

     

    1.证明：△=(m+2)2－4(2m－1)=m2－4m+8=(m－2)2+4     

    ∵(m－2)2≥0  ∴(m－2)2+4＞0        ∴方程有两个不相等的实数根

    2.存在实数m，使方程的两个实数根互为相反数.    由题知：x1+x2=－(m+2)=0

         解得：m = - 2          将m = - 2代入,解得:x=            

    ∴m的值为 - 2，方程的根为

     解析:略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学教研室 题型：044

    已知关于x的一元二次方程x2–(m2＋3)x＋ (m2＋2)＝0．

    （1）试证：无论m取任何实数，方程均有两个正实根；

    （2）设x1、x2为方程的两个实根，且满足x12＋x22–x1x2＝，求m的值

     

    查看答案和解析>>

    科目：初中数学 来源：中考模拟试卷 数学 题型：044

    如图，在半径为4的圆O中，AB，CD是两条直径，M是OB的中点，CM的延长线交圆O于点E，设DE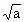＝(a＞0)，EM＝x．

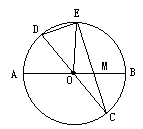
    (1)用含x和a的代数式表示MC的长，并试证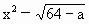·x＋12＝0；

    (2)当a＝15且EM＞MC时，求sin∠EOM；

    (3)根据图形写出EM长的取值范围；

    (4)试问，在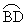上是否存在一点E，使EM的长是关于x的方程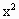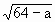－·x＋12＝0的相等的实根，如果存在，求出sin∠EOM的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    若a，b，c为△ABC的三边，且关于x的方程：4x2+4（a2+b2+c2）x+3（a2b2+b2c2+c2a2）=0有两个相等的实数根，试证△ABC是等边三角形．

    查看答案和解析>>

    同步练习册答案