

分析 (1)结论OD=OE.只要证明△OBD≌△OCE即可;
(2)由△OBD≌△OCE,推出S△OBD=S△OCE,推出S四边形ODBE=S△OBC=$\frac{1}{2}$S△ABC即可解决问题;
(3)当AD=3时,易证AD=BD=BE=CE,△AOD≌△COE;
(4)结论:OD=OE.只要证明△OBD≌△OCE即可;
解答 解:(1)如图①中,结论:OD=OE.理由如下: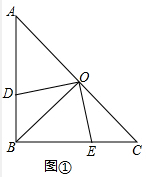
∵OA=OB=OC,
∴△ABC是直角三角形,
∴∠ABC=90°,
∵BA=BC,∠C=∠A=∠ABO=45°,OA=OC,
∴BO⊥AC,∵OE⊥OD,
∴∠BOC=∠DOE=90°,
∴∠DOB=∠EOC,
∵OB=OC,∠OBD=∠C,
∴△OBD≌△OCE,
∴OD=OE.
(2)四边形ODBE的面积不变.
理由:∵△OBD≌△OCE,
∴S△OBD=S△OCE,
∴S四边形ODBE=S△OBC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×6×6=9(cm2),
∴四边形ODBE的面积不变.
(3)当AD=3时,易证AD=BD=BE=CE,△AOD≌△COE.
故答案为3.
(4)如图2中,结论:OD=OE.理由如下: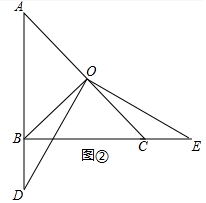
∵OA=OB=OC,
∴△ABC是直角三角形,
∴∠ABC=90°,
∵BA=BC,∠ACB=∠A=∠ABO=45°,OA=OC,
∴BO⊥AC,∵OE⊥OD,
∴∠BOC=∠DOE=90°,
∴∠DOB=∠EOC,
∵OB=OC,∠OBD=∠OCE=135°,
∴△OBD≌△OCE,
∴OD=OE.
点评 本题考查四边形综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、四边形面积问题等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 选手 | 课件制作 | 片段教学 | 综合素质 |
| 甲 | 85 | 78 | 85 |
| 乙 | 73 | 80 | 82 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
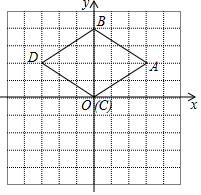 如图所示,△DBC是由△ABC经过变换得到的图形,分别写出点A、B、C、D的坐标,观察点A与点D的坐标之间的关系,如果△ABC中任一点N的坐标为N(x,y),它在△BCD中的对应点M的坐标是什么?
如图所示,△DBC是由△ABC经过变换得到的图形,分别写出点A、B、C、D的坐标,观察点A与点D的坐标之间的关系,如果△ABC中任一点N的坐标为N(x,y),它在△BCD中的对应点M的坐标是什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com