
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)当动点P在直线OB上时,点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,求PA:PC的值.



解:(1)∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
(2)过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示.
∵点A的纵坐标与点B的横坐标相等,
∴OA=AB.
∵∠OAB=90°,
∴∠AOB=∠ABO=45°.
∵∠AOC=90°,
∴∠POC=45°.
∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=90°.
∴∠NPM=90°.
∵∠APC=90°.
∴∠APN=90°﹣∠APM=∠CPM.
在△ANP和△CMP中,
∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.
∴PA=PC.
∴PA:PC的值为1:1.
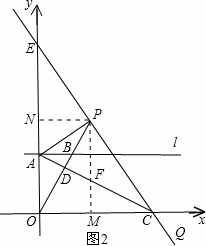
(3)①若点P在线段OB的延长线上,
过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,
PM与直线AC的交点为F,如图2所示.
∵∠APN=∠CPM,∠ANP=∠CMP,
∴△ANP∽△CMP.
∴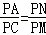 .
.
∵∠ACE=∠AEC,
∴AC=AE.
∵AP⊥PC,
∴EP=CP.
∵PM∥y轴,
∴AF=CF,OM=CM.
∴FM=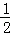 OA.
OA.
设OA=x,
∵PF∥OA,
∴△PDF∽△ODA.
∴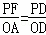
∵PD=2OD,
∴PF=2OA=2x,FM=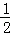 x.
x.
∴PM=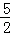 x.
x.
∵∠APC=90°,AF=CF,
∴AC=2PF=4x.
∵∠AOC=90°,
∴OC=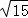 x.
x.
∵∠PNO=∠NOM=∠OMP=90°,
∴四边形PMON是矩形.
∴PN=OM=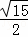 x.
x.
∴PA:PC=PN:PM=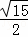 x:
x: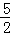 x=
x=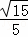 .
.
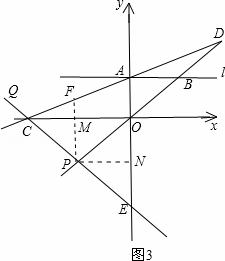
②若点P在线段OB的反向延长线上,
过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,
PM与直线AC的交点为F,如图3所示.
同理可得:PM=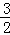 x,CA=2PF=4x,OC=
x,CA=2PF=4x,OC=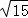 x.
x.
∴PN=OM=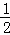 OC=
OC=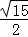 x.
x.
∴PA:PC=PN:PM=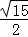 x:
x: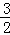 x=
x= .
.
综上所述:PA:PC的值为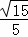 或
或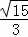 .
.





 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
2014年世界杯足球赛在巴西举行,小李在网上预订了小组赛和淘汰赛两个阶段的球票共10 张,总价为5800元.其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
张,总价为5800元.其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
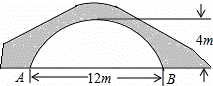


查看答案和解析>>
科目:初中数学 来源: 题型:
为了解某校七,八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调查,已知抽取七年级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表.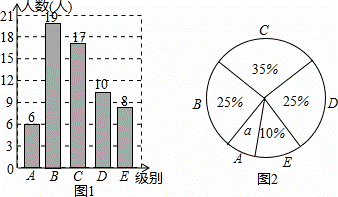
组别 睡眠时间x
A x≤7.5
B 7.5≤x≤8.5
C 8.5≤x≤9.5
D 9.5≤x≤10.5
E x≥10.5
根据图表提供的信息,回答下列问题:
(1)求统计图中的a;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为
A. 70° B. 80° C. 40° D. 30°
 |


查看答案和解析>>
科目:初中数学 来源: 题型:
某公司去年的营业额为四亿零七百万元,这个数据用科学记数法可表示为( )
A. 4.07×107元 B. 4.07×108元 C. 4.07×109元 D. 4.07×1010元


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com