
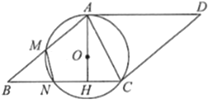
【题目】如图,点O是线段AH上一点,AH=3,以点O为圆心,OA的长为半径作⊙O,过点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作ABCD.
(1)求证:AD是⊙O的切线;
(2)若OH![]() AH,求四边形AHCD与⊙O重叠部分的面积;
AH,求四边形AHCD与⊙O重叠部分的面积;
(3)若NH![]() AH,BN
AH,BN![]() ,连接MN,求OH和MN的长.
,连接MN,求OH和MN的长.
【答案】(1)证明见解析;(2)![]() ;(3)OH
;(3)OH![]() ,MN
,MN![]() .
.
【解析】
(1)根据平行四边形的性质可知AD∥BC,证明OA⊥AD,又因为OA为半径,即可证明结论;
(2)利用锐角三角函数先求出∠OCH=30°,再求出扇形OAC的面积,最后求出△OHC的面积,两部分面积相加即为重叠部分面积;
(3)设⊙O半径OA=r=OC,OH=3-r,在Rt△OHC中,利用勾股定理求出半径r=![]() ,推出OH=
,推出OH=![]() ,再在Rt△ABH和Rt△ACH中利用勾股定理分别求出AB,AC的长,最后证△BMN∽△BCA,利用相似三角形对应边的比相等即可求出MN的长.
,再在Rt△ABH和Rt△ACH中利用勾股定理分别求出AB,AC的长,最后证△BMN∽△BCA,利用相似三角形对应边的比相等即可求出MN的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠AHC=90°,
∴∠HAD=90°,即OA⊥AD,
又∵OA为半径,
∴AD是⊙O的切线;
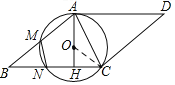
(2)如图,连接OC,
∵OH![]() OA,AH=3,
OA,AH=3,
∴OH=1,OA=2,
∵在Rt△OHC中,∠OHC=90°,OH![]() OC,
OC,
∴∠OCH=30°,
∴∠AOC=∠OHC+∠OCH=120°,
∴S扇形OAC![]() ,
,
∵CH![]() ,
,
∴S△OHC![]() 1
1![]() ,
,
∴四边形ABCD与⊙O重叠部分的面积=S扇形OAC+S△OHC![]() ;
;
(3)设⊙O半径OA=r=OC,OH=3﹣r,
在Rt△OHC中,OH2+HC2=OC2,
∴(3﹣r)2+12=r2,
∴r![]() ,则OH
,则OH![]() ,
,
在Rt△ABH中,AH=3,BH![]() 1
1![]() ,则AB
,则AB![]() ,
,
在Rt△ACH中,AH=3,CH=NH=1,得AC![]() ,
,
在△BMN和△BCA中,
∠B=∠B,∠BMN=∠BCA,
∴△BMN∽△BCA,
∴![]() 即
即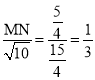 ,
,
∴MN![]() ,
,
∴OH![]() ,MN
,MN![]() .
.


科目:初中数学 来源: 题型:
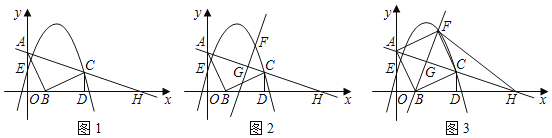
【题目】综合与探究:
如图1,![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及抛物线的表达式;
的坐标及抛物线的表达式;
(2)如图2,已知点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() (点
(点![]() 在第一象限),设点
在第一象限),设点![]() 的横坐标为
的横坐标为![]() .
.
①点![]() 的纵坐标用含
的纵坐标用含![]() 的代数式表示为________;
的代数式表示为________;
②如图3,当直线![]() 经过点
经过点![]() 时,求点
时,求点![]() 的坐标,判断四边形
的坐标,判断四边形![]() 的形状并证明结论;
的形状并证明结论;
③在②的前提下,连接![]() ,点
,点![]() 是坐标平面内的点,若以
是坐标平面内的点,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, ![]() ,
, ![]() 与
与![]() 成正比例,
成正比例, ![]() 与
与![]() 成反比例,并且当
成反比例,并且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根据![]() 与x成正比例,
与x成正比例, ![]() 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出![]() 和
和![]() 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
本题解析:
(![]() )设
)设![]() ,
, ![]() ,
,
则![]() ,
,
∵当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴
解得, ![]() ,
,
∴![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24
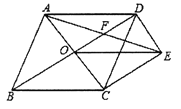
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
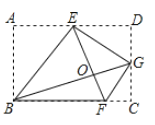
【题目】将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有A、B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.A、B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,请问A、B两种商品打折前各多少钱?打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
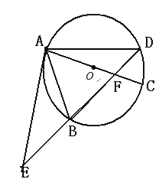
【题目】(本题满分8分)如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,
∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)在(2)的条件下,已知AF=4,CF=2,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com