
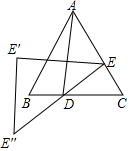
 如图,在等边△ABC中,AB=4,D是BC边上任意一点(不与B,C重合),过点D作DE⊥AC,垂足为E,作点E关于直线AD对称的点E',作点E关于点D的对称点E″,作△EE'E″,当△EE'E″是轴对称图形时,S△EE'E″=48-24$\sqrt{3}$.
如图,在等边△ABC中,AB=4,D是BC边上任意一点(不与B,C重合),过点D作DE⊥AC,垂足为E,作点E关于直线AD对称的点E',作点E关于点D的对称点E″,作△EE'E″,当△EE'E″是轴对称图形时,S△EE'E″=48-24$\sqrt{3}$. 分析 记AD与EE′交点为F,设BD=x,则CD=4-x,根据DE⊥AC且∠C=60°得DE=CDsinC=$\frac{\sqrt{3}(4-x)}{2}$、CE=CDcosC=$\frac{4-x}{2}$、AE=AC-CE=4-$\frac{4-x}{2}$=$\frac{4+x}{2}$,由点E与点E′关于AD对称、点E与点E″关于点D对称得EF=E′F、ED=E″D、∠DFE=90°,继而知DF∥E′E″、$\frac{DF}{E′E″}$=$\frac{1}{2}$,证△DFE∽△E″E′E得∠E′=∠DFE=90°,即△EE′E″为直角三角形,若△EE'E″是轴对称图形则△EE′E″为等腰直角三角形,从而根据AE=DE求得x的值,即可得DE、EF的长,从而求出S△DEF的值,最后根据$\frac{{S}_{△DFE}}{{S}_{△E″E′E}}$=$\frac{1}{4}$可得答案.
解答 解:记AD与EE′交点为F,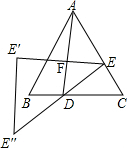
设BD=x,则CD=4-x,
∵DE⊥AC,且∠C=60°,
∴DE=CDsinC=$\frac{\sqrt{3}(4-x)}{2}$,CE=CDcosC=$\frac{4-x}{2}$,
则AE=AC-CE=4-$\frac{4-x}{2}$=$\frac{4+x}{2}$,
∵点E与点E′关于AD对称,点E与点E″关于点D对称,
∴EF=E′F,ED=E″D,且∠DFE=90°,
∴DF∥E′E″,且$\frac{DF}{E′E″}$=$\frac{1}{2}$,
∴△DFE∽△E″E′E,
∴∠E′=∠DFE=90°,即△EE′E″为直角三角形,
若△EE'E″是轴对称图形,
则△EE′E″为等腰直角三角形,
∴∠DEF=∠FDE=∠DAE=45°,
∴DE=AE,即$\frac{\sqrt{3}(4-x)}{2}$=$\frac{4+x}{2}$,
解得:x=8-4$\sqrt{3}$,
∵DE=$\frac{\sqrt{3}(4-x)}{2}$=6-2$\sqrt{3}$,
∴EF=DF=$\frac{\sqrt{2}}{2}$DE=3$\sqrt{2}$-$\sqrt{6}$,
则S△DEF=$\frac{1}{2}$DF•EF=$\frac{1}{2}$EF2=$\frac{1}{2}$×(3$\sqrt{2}$-$\sqrt{6}$)2=12-6$\sqrt{3}$,
∵△DFE∽△E″E′E,且$\frac{DF}{E′E″}$=$\frac{1}{2}$,
∴$\frac{{S}_{△DFE}}{{S}_{△E″E′E}}$=$\frac{1}{4}$,
∴S△EE'E″=4S△DEF=4×(12-6$\sqrt{3}$)=48-24$\sqrt{3}$,
故答案为:48-24$\sqrt{3}$.
点评 本题主要考查对称的性质、三角函数的应用、相似三角形的判定与性质及等边三角形的性质等知识点,根据对称的性质及中位线定理判断出△EE′E″为直角三角形及根据△EE'E″是轴对称图形得出△EE′E″为等腰直角三角形是解题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
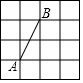 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
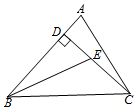 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积等于( )
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积等于( )| A. | 9 | B. | 13 | C. | 15 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com