
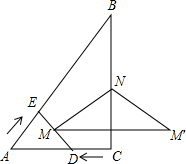
 如图,△ABC中,∠C=90°,AC=3,BC=4.点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,同时点E从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点E到达B点时D、E都停止运动.点M是DE的中点,直线MN⊥DE交直线BC于点N,点M′与M点关于直线BC对称.点D、E的运动时间为t(秒).
如图,△ABC中,∠C=90°,AC=3,BC=4.点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,同时点E从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点E到达B点时D、E都停止运动.点M是DE的中点,直线MN⊥DE交直线BC于点N,点M′与M点关于直线BC对称.点D、E的运动时间为t(秒).分析 (1)由点D的速度得出CD为1,得出AD=3-1=2,得出△ADE的面积即可;
(2)根据四边形BCDE的面积=△ABC的面积-△ADE的面积列出关系式即可;
(3)根据直线MN与△ABC的一边垂直满足的条件,解答即可;
(4)根据△MNM′为等腰直角三角形满足的条件计算即可.
解答 解:(1)∵点D从C点出发沿射线CA以每秒1个单位长度的速度匀速运动,
∴当t=1时,CD=1,
∴AD=AC-CD=3-1=2,
同理可得AE=1,
∵∠C=90°,AC=3,BC=4,
∴AB=5,
∴sin∠A=$\frac{4}{5}$,
∴△ADE的面积=$\frac{1}{2}×1×2×\frac{4}{5}$=$\frac{4}{5}$;
故答案为:2;$\frac{4}{5}$;
(2)设四边形BCDE的面积为S,
当0<t<3时,四边形BCDE的面积=△ABC的面积-△ADE的面积
=$\frac{1}{2}×3×4-\frac{1}{2}×\frac{4}{5}×t×(3-t)$
=6-$\frac{2}{5}t(3-t)$,
可得S与t的函数关系式是:S=6-$\frac{2}{5}$t(3-t);
(3)当直线MN与△ABC的一边垂直时,
应该满足t:(3-t)=5:3
解得:t=$\frac{15}{8}$;
(4)当∠EDA=45°时,△MNM′为等腰直角三角形.
$3-t-\frac{3}{5}t=\frac{4}{5}t$,
解得:t=$\frac{5}{4}$.
点评 此题主要考查了四边形的动点问题,等腰三角形的性质以及三角形的面积计算是中考中重点内容,同学们应熟练掌握并应用.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.
如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,∠BCA=75°,∠ABC=45°,AB=6$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,当线段EF长度取最小值时,CD=12-6$\sqrt{3}$.
如图,△ABC中,∠BCA=75°,∠ABC=45°,AB=6$\sqrt{2}$,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,当线段EF长度取最小值时,CD=12-6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为($\sqrt{3}$,1),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为($\sqrt{3}$,1),则点C的坐标为( )| A. | (-$\sqrt{3}$,1) | B. | (-1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (1,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com