练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．一条开口向下的抛物线的顶点坐标是（2，3），则这条抛物线有（　　）
    A．最大值3B．最小值3C．最大值2D．最小值-2

    分析 利用二次函数的性质求解．

    解答 解：∵抛物线开口向下，
    ∴二次函数有最大值，
    当x=2时，二次函数值最大，最大值为3．
    故选A．

    点评 本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），对称轴直线x=-$\frac{b}{2a}$．熟练掌握二次函数的性质是解决此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．已知动点P以每秒2cm的速度沿图甲的边框按B⇒C⇒D⇒E⇒F⇒A的路径移动，相应的三角形ABP的面积S（cm2）与时间t（秒）之间的关系用图乙中的图象表示，若AB=6cm，试回答下列问题：
    （1）图甲中的BC长是多少？
    （2）图乙中的a是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，在△ABD中，C是BD上一点，若E、F分别是AC、AB的中点，△DEF的面积为4.5，则△ABC的面积为18．

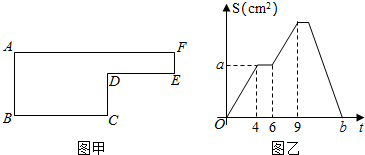
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，在矩形ABCD中，AD=3，AB＞3，AG平分∠BAD，分别过点B、C作BE⊥AG于点E，CF⊥AG于点F，则（AE-GF）的值为（　　）
    A．3B．$\frac{{3\sqrt{2}}}{2}$C．$\frac{{3\sqrt{3}}}{2}$D．$3\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如果一个空间几何体的主视图和左视图都是边长为4的正三角形，俯视图是圆且中间有一点，那么这个几何体的表面积是（　　）
    A．8πB．12πC．4$\sqrt{3}$πD．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

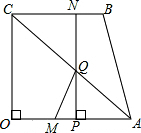    15．如图，四边形OABC为直角梯形，OA∥BC，∠AOC=90°，OA=OC=4，BC=3．点M从O出发以每秒2个单位长度的速度向A运动；点N从B同时出发，以每秒1个单位长度的速度向C运动，当其中一个动点达到终点时，另一个动点也随之停止运动，过点N作NP垂直OA于点P，连接AC交NP于点Q，连接MQ．
    （1）当t为何值时，M和P两点重合；
    （2）求△AQM的面积S与运动时间t的函数关系式，并写出自变量t的取值范围，及当t为何值时，S的值最大；
    （3）是否存在点M，使得△AQM为直角三角形？若存在，求NQ的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，在四边形ABCD中，AC=a，BD=b，且AC⊥BD顺次连接四边形ABCD各边的中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2…，如此进行下去，得到四边形AnBnCnDn．下列结论正确的有②③．
    ①四边形A2B2C2D2是矩形；
    ②四边形A4B4C4D4是菱形；
    ③四边形A5B5C5D5的周长是$\frac{a+b}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．计算：${（\sqrt{3}-1）^0}-{（\frac{1}{2}）^{-2}}-|{-3}|$=-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

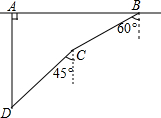    20．近年来，我国南海诸岛不断受到外国非法骚扰，为此，我军经常会做针对性海上演习，如图，在一次军事演习中，蓝方在一条东西轴向的公路上的A处朝正南方向撤退，红方在公路上的B处沿南偏西60°方向前进实施拦截，红方行驶1000米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方，求拦截点D处到公路的距离（结果不取近似值）．

    查看答案和解析>>

    同步练习册答案