
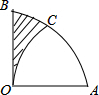
 如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$.
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作$\widehat{OC}$交$\widehat{AB}$于点C,若OA=2,则阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}π$. 分析 连接OC、AC,根据题意得到△AOC为等边三角形,∠BOC=30°,分别求出扇形COB的面积、△AOC的面积、扇形AOC的面积,计算即可.
解答 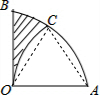 解:连接OC、AC,
解:连接OC、AC,
由题意得,OA=OC=AC=2,
∴△AOC为等边三角形,∠BOC=30°,
∴扇形COB的面积为:$\frac{30×π×{2}^{2}}{360}$=$\frac{1}{3}π$,
△AOC的面积为:$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
扇形AOC的面积为:$\frac{60×π×{2}^{2}}{360}$=$\frac{2π}{3}$,
则阴影部分的面积为:$\frac{1}{3}π$+$\sqrt{3}$-$\frac{2π}{3}$=$\sqrt{3}$-$\frac{1}{3}π$,
故答案为:$\sqrt{3}$-$\frac{1}{3}π$.
点评 本题考查的是扇形面积计算,掌握等边三角形的性质、扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
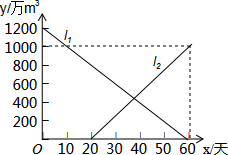 由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
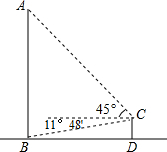 全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为58米(参考数据:tan78°12′≈4.8).
全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为11°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为58米(参考数据:tan78°12′≈4.8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com