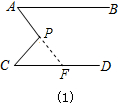
结论:(1)∠APC=∠A+∠C;
证明:延长AP交CD于点F,
∵AB∥CD,
∴∠PFC=∠A,
∵∠APC=∠PFC+∠C,
∴∠APC=∠A+∠C;
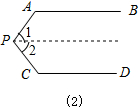
(2)∠A+∠P+∠C=360°.
证明:如图(2),过P作PE∥AB,则PE∥CD,
∴∠A+∠1=180°,∠C+∠2=180°,
∴∠APC+∠A+∠C=∠1+∠2+∠A+∠C=360°,∠A+∠P+∠C=360°;
(3)∠P=∠C-∠A;
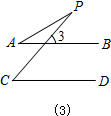
证明:∵AB∥CD,
∴∠3=∠C,
∵∠3=∠APC+∠A,
∴∠APC=∠C-∠A.
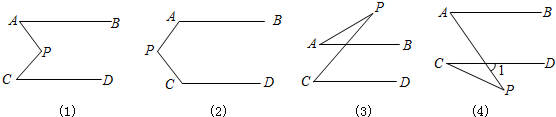
(4)∠P=∠A-∠C.
证明:如图(4)所示,
∵AB∥CD,
∴∠A=∠1,
∵∠1=∠P+∠C,
∴∠P=∠1-∠C=∠A-∠C.
分析:(1)延长AP交CD于点F,根据两直线平行,内错角相等可以得到∠A=∠PFC,再根据三角形的一个外角等于和它不相邻的两个内角的和即可得到∠APC=∠A+∠C;
(2)过P作PE∥AB,根据两直线平行,同旁内角互补可以得到∠A+∠1=180°,∠C+∠2=180°,所以∠P+∠A+∠C=360°;
(3)根据两直线平行,内错角相等可以得到∠4=∠C,再根据三角形的一个外角等于和它不相邻的两个内角的和即可得到∠APC=∠C-∠A;
(4)先根据AB∥CD可得出∠A=∠1,再由三角形外角的性质得出∠1=∠P+∠C,即∠P=∠1-∠C=∠A-∠C,故可得出结论.
点评:本题考查的是平行线的性质,根据题意作出辅助线,利用平行线的性质求解是解答此题的关键.

 结论:(1)∠APC=∠A+∠C;
结论:(1)∠APC=∠A+∠C;
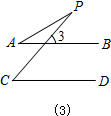


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案