练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.

    【答案】35°或145°．

    【解析】

    分两种情况讨论：点F在AO上，点F在OB上，依据平行线的性质以及角平分线的定义，即可得到∠AFG度数．

    解：如图，当点F在AO上时，

    ∵∠AOD＝110°，

    ∴∠AOC＝70°，

    又∵OE平分∠AOC，

    ∴∠COE＝35°，

    ∵FG∥OE，

    ∴∠OGF＝35°，

    ∴∠AFG＝∠AOD＋∠OGF＝110°＋35°＝145°；

    如图，当点F在OB上时，

    ∵∠AOD＝110°，

    ∴∠AOC＝70°，

    又∵OE平分∠AOC，

    ∴∠AOE＝35°，

    ∵FG∥OE，

    ∴∠AFG＝∠AOE＝35°，

    故答案为：35°或145°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】数学实验室：

    点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a﹣b|．

    利用数形结合思想回答下列问题：

    （1）数轴上表示2和5的两点之间的距离是_________，数轴上表示1和－3的两点之间的距离是 ；

    （2）数轴上若点A表示的数是x，点B表示的数是－2，则点A和B之间的距离是 ，若AB＝2，那么x为 ；

    （3）当x是 时，代数式；

    （4）若点A表示的数－1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，求运动几秒后，PQ＝1？（请写出必要的求解过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】股民小杨上星期五买进某公司股票 1000 股，每股 27 元．下表为本周内每日该股票的涨跌情况（单位：元）：

    （1）星期三收盘时，该股票涨或跌了多少元？

    （2）本周内该股票的最高价是每股多少元？最低价是每股多少元？

    （3）已知小杨买进股票时付了 1.5‰的手续费，卖出时还需要付成交额的 1.5‰的手续费和 1‰的交易税．如果小杨在星期五收盘前将全部股票卖出，则他的收益情况如何？

    （收益＝卖股票收入﹣买股票支出﹣卖股票手续费和交易税﹣买股票手续费）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=（x﹣3）（x+1）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．

    （1）求点B及点D的坐标．

    （2）连结BD，CD，抛物线的对称轴与x轴交于点E．

    ①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．

    ②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD的边BC上有一动点E，连接AE、DE，以AE、DE为边作AEDF．在点E从点B移动到点C的过程中，AEDF的面积（ ）

    A.先变大后变小B.先变小后变大C.一直变大D.保持不变

    查看答案和解析>>

    科目：初中数学 来源： 题型：

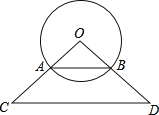
    【题目】已知⊙O的半径为12cm，弦AB=12cm．

    (1)求圆心O到弦AB的距离．

    (2)若弦AB恰好是△OCD的中位线，以CD中点E为圆点，R为半径作⊙E，当⊙O和⊙E相切时，求R的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

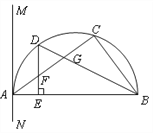
    【题目】如图，△ABC内接于半圆，AB是直径，过A作直线MN，若∠MAC＝∠ABC．

    （1）求证：MN是半圆的切线；

    （2）设D是弧AC的中点，连结BD交AC 于G，过D作DE⊥AB于E，交AC于F．求证：FD＝FG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A、B在数轴上分别表示数a，b．若A、B两点间的距离记为d，则d和a，b之间的数量关系是d=|a-b|.

    (1)数轴上有理数x与有理数－2所对应两点之间的距离可以表示为______；

    (2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离；

    若|x+6|= |x -2|，则x=______；

    (3)若a=1，b=-2，将数轴折叠，使得A点与﹣7表示的点重合，则B点与数______表示的点P重合；

    (4)若数轴上M、N两点之间的距离为11(M在N的左侧)，且M、N两点经过(3)中折叠后互相重合，则M、N两点表示的数分别是：M：_____， N：_______；

    (5)在题(3)的条件下，点A为定点，点B、P为动点，若移动点B、P中一点后，能否使相邻两点间距离相等？若能，请写出移动方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料并解决有关问题：

    我们知道：|x|＝．现在我们可以用这一结论来化简含有绝对值的代数式，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1＝0和x﹣2＝0，分别求得x＝﹣1，x＝2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x＝﹣1和，x＝2可将全体实数分成不重复且不遗漏的如下3种情况：

    ①x＜﹣1；②﹣1≤x＜2；③x≥2．

    从而化简代数式|x+1|+|x﹣2|可分以下3种情况：

    ①当x＜﹣1时，原式＝﹣（x+1）﹣（x﹣2）＝﹣2x+1；

    ②当﹣1≤x＜2时，原式＝x+1﹣（x﹣2）＝3；

    ③当x≥2时，原式＝x+1+x﹣2＝2x﹣1．综上讨论，原式＝．

    通过以上阅读，请你解决以下问题：

    （1）化简代数式|x+2|+|x﹣4|．

    （2）求|x﹣1|﹣4|x+1|的最大值．

    查看答案和解析>>

    同步练习册答案