练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（　　）

    A．  c＞﹣1        Bb＞0            C．2a+b≠0       D． 9a+c＞3b


    D             解：∵抛物线与y轴的交点在点（0，﹣1）的下方．

    ∴c＜﹣1；

    故A错误；

    ∵抛物线开口向上，

    ∴a＞0，

    ∵抛物线的对称轴在y轴的右侧，

    ∴x=﹣＞0，

    ∴b＜0；

    故B错误；

    ∵抛物线对称轴为直线x=﹣，

    ∴若x=1，即2a+b=0；

    故C错误；

    ∵当x=﹣3时，y＞0，

    ∴9a﹣3b+c＞0，

    即9a+c＞3b．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，能判定EB∥AC的条件是（　　）

    A．  ∠C=∠ABE     B．∠A=∠EBD     C．∠C=∠ABC     D． ∠A=∠ABE

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知直线AB和CD相交于点O，∠AOC为锐角，过O点作直线OE、OF．若∠COE=90°，OF平分∠AOE，求∠AOF+∠COF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    对于二次函数y=ax2﹣（2a﹣1）x+a﹣1（a≠0），有下列结论：

    ①其图象与x轴一定相交；

    ②若a＜0，函数在x＞1时，y随x的增大而减小；

    ③无论a取何值，抛物线的顶点始终在同一条直线上；

    ④无论a取何值，函数图象都经过同一个点．

    其中所有正确的结论是　　．（填写正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


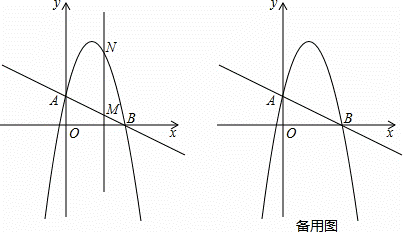
    如图，一次函数y=﹣x+2分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点．

    （1）求这个抛物线的解析式；

    （2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？

    （3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将抛物线y=（x﹣1）2+3向左平移1个单位，得到的抛物线与y轴的交点坐标是（　　）

    A．  （0，2）      B．（0，3）      C．（0，4）      D． （0，7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    请写出一个以直线x=﹣2为对称轴，且在对称轴左侧部分是上升的抛物线的表达式，这条抛物线的表达式可以是　  等　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果m是任意实数，则点P（m，1﹣2m）一定不在（　　）

    A．  第一象限      B．第二象限      C．第三象限      D． 第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    甲、乙两人以相同路线前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以下说法：①乙比甲提前12分钟到达；②甲的平均速度为15千米/小时；③乙走了8km后遇到甲；④乙出发6分钟后追上甲．其中正确的有（　　）

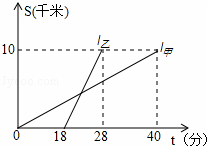
    A．  4个           B．3个           C．2个           D． 1个

    查看答案和解析>>

    同步练习册答案