
 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )| A. | ∠B=∠B′ | B. | PA=PA′ | ||
| C. | BC=AA′ | D. | MN是线段AA′的垂直平分线 |
科目:初中数学 来源: 题型:解答题
 如图,△ABC与△A1B1C1是位似图形.
如图,△ABC与△A1B1C1是位似图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
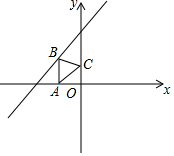 如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )
如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )| A. | $\sqrt{10}$ | B. | 2+$\sqrt{2}$ | C. | 1-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{3}$ | D. | 1-$\frac{\sqrt{2}+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.
某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的两个角是对顶角 | |
| B. | 老师测量跳远成绩的依据是两点之间,线段最短 | |
| C. | 从直线外一点到这条直线上的各点所连接的线段中,垂线段最短 | |
| D. | 一个角一定不等于它的余角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com