
【题目】如图,已知函数y=x+2的图象与函数y=![]() (k≠0)的图象交于A、B两点,连接BO并延长交函数y=
(k≠0)的图象交于A、B两点,连接BO并延长交函数y=![]() (k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
(k≠0)的图象于点C,连接AC,若△ABC的面积为8.则k的值为_____.
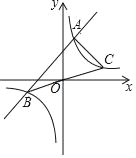
【答案】3
【解析】
连接OA.根据反比例函数的对称性可得OB=OC,那么S△OAB=S△OAC=![]() S△ABC=4.求出直线y=x+2与y轴交点D的坐标.设A(a,a+2),B(b,b+2),则C(-b,-b-2),根据S△OAB=4,得出a-b=4①.根据S△OAC=4,得出-a-b=2②,①与②联立,求出a、b的值,即可求解.
S△ABC=4.求出直线y=x+2与y轴交点D的坐标.设A(a,a+2),B(b,b+2),则C(-b,-b-2),根据S△OAB=4,得出a-b=4①.根据S△OAC=4,得出-a-b=2②,①与②联立,求出a、b的值,即可求解.
如图,连接OA.
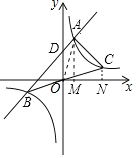
由题意,可得OB=OC,
∴S△OAB=S△OAC=![]() S△ABC=4.
S△ABC=4.
设直线y=x+2与y轴交于点D,则D(0,2),
设A(a,a+2),B(b,b+2),则C(-b,-b-2),
∴S△OAB=![]() ×2×(a-b)=4,
×2×(a-b)=4,
∴a-b=4 ①.
过A点作AM⊥x轴于点M,过C点作CN⊥x轴于点N,
则S△OAM=S△OCN=![]() k,
k,
∴S△OAC=S△OAM+S梯形AMNC-S△OCN=S梯形AMNC=4,
∴![]() (-b-2+a+2)(-b-a)=4,
(-b-2+a+2)(-b-a)=4,
将①代入,得
∴-a-b=2 ②,
①+②,得-2b=6,b=-3,
①-②,得2a=2,a=1,
∴A(1,3),
∴k=1×3=3.
故答案为3.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】观察下表:

则一元二次方程x2-2x-2=0在精确到0.1时一个近似根是______,利用抛物线的对称性,可推知该方程的另一个近似根是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某大学的楼门是一抛物线形水泥建筑物,大门的地面宽度为![]() ,两侧距离地面
,两侧距离地面![]() 高处各有一个挂校名横匾用的铁环,两铁环的水平距离为
高处各有一个挂校名横匾用的铁环,两铁环的水平距离为![]() ,则校门的高约为(精确到
,则校门的高约为(精确到![]() ,水泥建筑物的厚度忽略不计)( )
,水泥建筑物的厚度忽略不计)( )
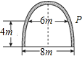
A. 9.2m B. 9.1m C. 9.0m D. 8.9m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )

A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知MN∥EF∥BC,点A、D为直线MN上的两动点,AD=a,BC=b,AE∶ED=m∶n;
(1)当点A、D重合,即a=0时(如图1),试求EF.(用含m,n,b的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当A、D不重合,即a≠0,
①如图2这种情况时,试求EF.(用含a,b,m,n的代数式表示)
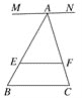
图1
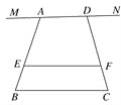
图2
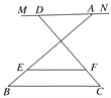
图3
②如图3这种情况时,试猜想EF与a、b之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,△ABC经过平移后得到△A1B1C1,若AC上一点P(1.2,1.4)平移后对应点为P1,点P1绕原点顺时针旋转180°,对应点为P2,则点P2的坐标为( )
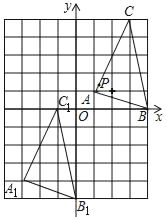
A. (2.8,3.6) B. (﹣2.8,﹣3.6)
C. (3.8,2.6) D. (﹣3.8,﹣2.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )
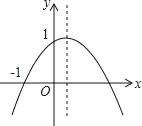
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
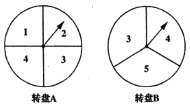
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由传动的转盘A,B分别分成4等份,3等份的扇形区域,并在每一小区域内标上数字(如图所示).游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为奇数,则甲胜;若指针所指两个区域的数字之和为偶数,则乙胜.如果指针落在分割线上,则需要重新转动转盘.请问这个游戏规则对甲、乙双方公平吗?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com