Question

（2012•嘉定区二模）已知△ABC中，∠ACB=90°（如图），点P到∠ACB两边的距离相等，且PA=PB．
（1）先用尺规作出符合要求的点P（保留作图痕迹，不需要写作法），然后判断△ABP的形状，并说明理由；
（2）设PA=m，PC=n，试用m、n的代数式表示△ABC的周长和面积；
（3）设CP与AB交于点D，试探索当边AC、BC的长度变化时，

CD

AC

+

CD

BC

的值是否发生变化，若不变，试求出这个不变的值，若变化，试说明理由．

Answer 1

分析：（1）先根据角平分线及线段垂直平分线的作法作出P点，过点P分别作PE⊥AC、PF⊥CB，垂足为E、F，由全等三角形的判定定理得出Rt△APE≌Rt△BPF，再由全等三角形的性质即可判断出△ABP是等腰直角三角形；
（2）在Rt△PAB中，由∠APB=90°，PA=PB，PA=m，可得出AB=

2

m，由Rt△APE≌Rt△BPF，△PCE≌△PCF，可得AE=BF，CE=CF，故CA+CB=CE+EA+CB=CE+CF=2CE，在Rt△PCE中，∠PEC=90°，∠PCE=45°，PC=n，可知CE=PE=

2

2

n，即CA+CB=2CE=

2

n，由△ABC的周长为=AB+BC+CA即可得出其周长，再根据S_△ABC=S_△PAC+S_△PBC-S_△PAB即可得出其面积；
（3）过点D分别作DM⊥AC、DN⊥BC，垂足为M、N，由角平分线的定义及锐角三角函数的定义可知DM=DN=CDsin45°=

2

2

CD，由平行线分线段成比例定理可知

DN

AC

=

DB

AB

，

DM

BC

=

AD

AB

，再把两式相加即可得出结论．

解答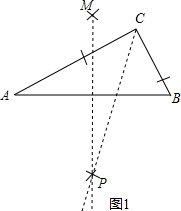：解：（1）依题意，点P既在∠ACB的平分线上，又在线段AB的垂直平分线上．
如图1，作∠ACB的平分线CP，作线段AB的垂直平分线PM，CP与PM的交点即为所求的P点．
△ABP是等腰直角三角形．
理由如下：过点P分别作PE⊥AC、PF⊥CB，垂足为E、F（如图2）．
∵PC平分∠ACB，PE⊥AC、PF⊥CB，垂足为E、F，
∴PE=PF．
在Rt△APE与Rt△BPF中，
∵

PE=PF PA=PB

，
∴Rt△APE≌Rt△BPF．
∴∠APE=∠BPF，
∵∠PEC=90°，∠PFC=90°，∠ECF=90°，
∴∠EPF=90°，
∴∠APB=90°．
又∵PA=PB，
∴△ABP是等腰直角三角形．

（2）如图2，∵在Rt△PAB中，∠APB=90°，PA=PB，PA=m，
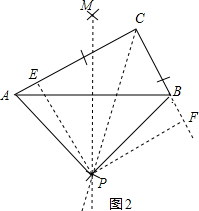
∴AB=

2

m，
由Rt△APE≌Rt△BPF，△PCE≌△PCF，可得AE=BF，CE=CF，
∴CA+CB=CE+EA+CB=CE+CF=2CE，
在Rt△PCE中，∠PEC=90°，∠PCE=45°，PC=n，
∴CE=PE=

2

2

n，
∴CA+CB=2CE=

2

n，
∴△ABC的周长为=AB+BC+CA=

2

m+

2

n．
∵S_△ABC=S_△PAC+S_△PBC-S_△PAB
=

1

2

AC•PF+

1

2

BC•PF-

1

2

PA•PB
=

1

2

（AC+BC）•PE-

1

2

PA²
=

1

2

×

2

n×

2

2

n-

1

2

m²
=

1

2

n²-

1

2

m²（n＞m）．
[或 S_△ABC=

1

2

AC•BC=

1

4

[（AC+BC）²-（AC²+BC²）]=

1

2

（n²-m²）]

（3）不变．
【法1】过点D分别作DM⊥AC、DN⊥BC，垂足为M、N（图3）．
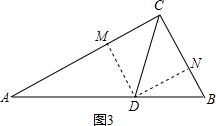
易得 DM=DN=CDsin45°=

2

2

CD，
由DN∥AC得

DN

AC

=

DB

AB

①；
由DM∥BC得

DM

BC

=

AD

AB

②，
①+②，得

DN

AC

+

DM

BC

=

DB+AD

AB

，即

DN

AC

+

DM

BC

=1
∴

2

2

（

CD

AC

+

CD

BC

）=1，即

CD

AC

+

CD

BC

=

2

；
【法2】（前面同法1）又∵S_△ABC=S_△ACD+S_△BCD，S_△ABC=

1

2

AC•BC
∴S_△ACD=S_△BCD=

1

2

AC•DM+

1

2

BC•DN=

1

2

（AC+BC）•

2

2

CD
∴

1

2

（AC+BC）•

2

2

CD=

1

2

AC•BC
∴

(AC+BC)CD

AC•BC

=

2

，即

CD

AC

+

CD

BC

=

2

；
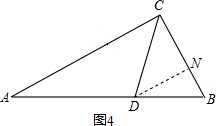
【法3】过点D作DN⊥BC，垂足为N（图4）．
在Rt，CDN中，∠DCN=45°，DN=CN=

2

2

CD，
由DN∥AC得

DN

AC

=

DB

AB

①；

CN

BC

=

AD

AB

②
①+②，得

DN

AC

+

CN

BC

=

DB+AD

AB

，即

DN

AC

+

CN

BC

=1
则

2

2

（

CD

AC

+

CD

BC

）=1，即

CD

AC

+

CD

BC

=

2

；
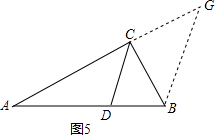
【法4】过点B作BG∥DC，交射线AC于点G（如图5）
易得∠G=∠ACD=∠BCD=∠CBG=45°，BG=

2

BC=

2

CG．
∵BG∥DC，
∴

BG

CD

=

AG

AC

，
∴

2 BC

CD

=

AC+BC

AC

，

(AC+BC)•CD

AC•BC

=

2

，
即

CD

AC

+

CD

BC

=

2

；

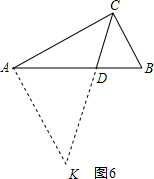
【法5】过点A作CB的平行线，交射线CD于点K（见图6），
得CK=

2

AC，DK=CK-CD=

2

AC-CD，
又

CD

BC

=

DK

AK

，即

CD

BC

=

2 AC-CD

AC

，
所以

CD

BC

=

2

-

CD

AC

，即

CD

AC

+

CD

BC

=

2

；
【法6】分别过点A、B分别作CD的平行线，交射线BC于点H，交射线AC于点G（见图7）．
得AH=

2

AC，BG=

2

BC，
又∵

CD

BG

=

AD

AB

，

CD

AH

=

BD

AB

∴

CD

AH

+

CD

BG

=1，
即

CD

2 AC

+

CD

2 BC

=1，即

CD

AC

+

CD

BC

=

2

；

点评：本题考查的是相似形综合题，涉及到角平分线及线段垂直平分线的作法及性质、平行线的性质、全等三角形的判定与性质及三角形的面积公式，涉及面较广，难度较大．