
分析 (1)根据平均数、方差的含义和求法,分别求出A,B两种品牌冰箱数据的平均数和方差即可.
(2)方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,据此比较该商场1-5月这两种品牌冰箱月销售量的稳定性即可.
解答 解:(1)A品牌冰箱数据的平均数为:$\frac{1}{5}$×(15+16+17+13+14)=15(台)
B品牌冰箱数据的平均数为:$\frac{1}{5}$×(10+14+15+20+16)=15(台)
S2A品牌=$\frac{1}{5}$×[(15-15)2+(16-15)2+(17-15)2+(13-15)2+(14-15)2]
=$\frac{1}{5}$×[0+1+4+4+1]
=2
S2B品牌=$\frac{1}{5}$×[(10-15)2+(14-15)2+(15-15)2+(20-15)2+(16-15)2]
=$\frac{1}{5}$×[25+1+0+25+1]
=10.4
(2)∵2<10.4,
∴S2A品牌<S2B品牌,
∴该商场1-5月A品牌冰箱月销售量更为稳定.
点评 此题主要考查了方差的含义和求法,要熟练掌握,解答此题的关键是要明确:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
| 平均数(分) | 中位数(分) | 众数(分) |
| 3.4 | 4 | 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
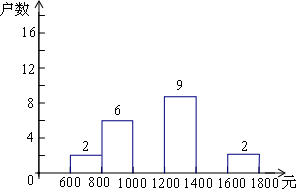 小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.| 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | a | 40% |
| 1200≤x<1400 | 9 | 22.5% |
| 1400≤x<1600 | b | c |
| 1600≤x<1800 | 2 | 5% |
| 合计 | 40 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
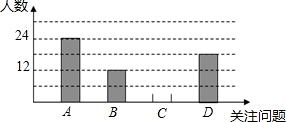 6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:
6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:| 关注问题 | 频数 | 频率 |
| A | 24 | b |
| B | 12 | 0.2 |
| C | n | 0.1 |
| D | 18 | m |
| 合计 | a | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com