Question

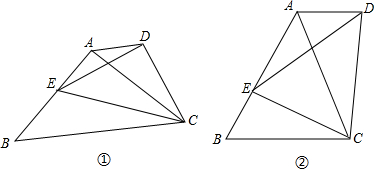
如图，已知在等腰△ABC中，∠A＝∠B＝30°，过点C作CD⊥AC交AB于点D．

(1)尺规作图：过A、D、C三点作⊙O(只要求作出图形，保留痕迹，不要求写作法)；

(2)求证：BC是过A、D、C三点的圆的切线；

(3)若过A、D、C三点的圆的半径为，则线段BC上是否存在一点P，使得以P、D、B为顶点的三角形与△BCO相似．若存在，求出DP的长；若不存在，请说明理由．

Answer 1

答案：
解析：

解：(1)作出圆心O(即AD的中点)，以点O为圆心，OA长为半径作圆． 　　(2)证明：因为CD⊥AC， 　　所以∠ACD＝90°． 　　所以AD是⊙O的直径． 　　连接OC， 　　因为∠A＝∠B＝30°， 　　所以∠ACB＝120°． 　　又因为OA＝OC， 　　所以∠ACO＝∠A＝30°． 　　所以∠BCO＝∠ACB－∠ACO＝120°－30°＝90°． 　　所以BC⊥OC． 　　所以BC是⊙O的切线． 　　(3)存在． 　　因为∠BCD＝∠ACB－∠ACD＝120°－90°＝30°， 　　所以∠BCD＝∠B，即DB＝DC． 　　又因为在Rt△ACD中，DC＝AD·sin30°＝， 　　所以BD＝． 　　①当△BP1D∽△BCO时，∠DP1B＝∠OCB＝90°． 　　在Rt△BP1D中， 　　DP1＝BD·sin30°＝． 　　②当△BDP2∽△BCO时，∠P2DB＝∠OCB＝90°． 　　在Rt△BDP2中，DP2＝BD·tan30°＝1．