
分析 (1)数轴三要素:原点,单位长度,正方向.依此表示出家以及A、B、C三个村庄的位置;
(2)距离相加的和即为所求;
(3)分两种情况:①D村在C村左边时;②D村在C村右边时;分别计算即可.
解答 解:(1)如图所示: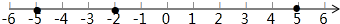
(2)2+3+10=15,即小明一共走了15千米;
(3)分两种情况:①D村在C村左边时,
则C、D村表示的数分别是5千米、4千米,
4-(-2-3)=4+5=9(千米);
②D村在C村右边时,
则C、D村表示的数分别是5千米、6千米,
6-(-2-3)=6+5=11(千米);
综上所述:D到B村有9千米或11千米.
点评 本题考查的是数轴、绝对值的有关内容,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:填空题
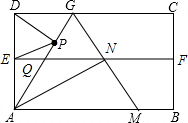 如图,四边形ABCD是矩形纸片,AD=2$\sqrt{3}$,对折矩形纸片ABCD,使AB与CD重合,折痕为EF;展平后再过点A折叠矩形纸片,使点D落在EF上的点N,折痕AG与EF相交于点Q;再次展平,连接AN,GN,延长GN交AB于点M,有如下结论:
如图,四边形ABCD是矩形纸片,AD=2$\sqrt{3}$,对折矩形纸片ABCD,使AB与CD重合,折痕为EF;展平后再过点A折叠矩形纸片,使点D落在EF上的点N,折痕AG与EF相交于点Q;再次展平,连接AN,GN,延长GN交AB于点M,有如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2或-2 | D. | -2或-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com