

分析 (1)①根据“两点之间,线段最短”可知:线段A′B为最近路线;
②Ⅰ.将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①,运用勾股定理求出AC长;Ⅱ.将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②,运用勾股定理求出A′C长,然后将两个长度进行比较,就可解决问题;
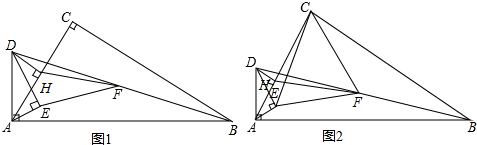
(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.由⊙M与PQ相切于点Q可得MQ⊥PQ,即∠MQP=90°,根据勾股定理可得PQ=$\sqrt{M{P}^{2}-M{Q}^{2}}$=$\sqrt{M{P}^{2}-100}$.要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
解答 解:(1)①根据“两点之间,线段最短”可知:
线段A′B为最近路线,如图1所示.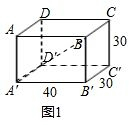
②Ⅰ.将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①.
在Rt△A′B′C中,
∠B′=90°,A′B′=40,B′C=60,
∴AC=$\sqrt{4{0}^{2}+6{0}^{2}}$=$\sqrt{5200}$=20$\sqrt{13}$.
Ⅱ.将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②.
在Rt△A′C′C中,
∠C′=90°,A′C′=70,C′C=30,
∴A′C=$\sqrt{7{0}^{2}+3{0}^{2}}$=$\sqrt{5800}$=10$\sqrt{58}$.
∵$\sqrt{5200}$<$\sqrt{5800}$,
∴往天花板ABCD爬行的最近路线A′GC更近;
(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.
∵半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,BC′=60dm,
∴MH=60-10=50,HB=15,AH=40-15=25,
根据勾股定理可得AM=$\sqrt{A{H}^{2}+M{H}^{2}}$=$\sqrt{2{5}^{2}+5{0}^{2}}$=$\sqrt{3125}$,
MB=$\sqrt{B{H}^{2}+M{H}^{2}}$=$\sqrt{1{5}^{2}+5{0}^{2}}$=$\sqrt{2725}$,
∴50≤MP≤$\sqrt{3125}$.
∵⊙M与PQ相切于点Q,
∴MQ⊥PQ,∠MQP=90°,
∴PQ=$\sqrt{M{P}^{2}-M{Q}^{2}}$=$\sqrt{M{P}^{2}-100}$.
当MP=50时,PQ=$\sqrt{2400}$=20$\sqrt{6}$;
当MP=$\sqrt{3125}$时,PQ=$\sqrt{3025}$=55.
∴PQ长度的范围是20$\sqrt{6}$dm≤PQ≤55dm.
点评 本题主要考查了两点之间线段最短、点到直线之间垂线段最短、切线的性质、长方体的展开图、勾股定理等知识,把空间图形的最短距离问题转化为到同一平面内最短距离问题是解决(1)②小题的关键,根据PQ=$\sqrt{M{P}^{2}-M{Q}^{2}}$把求PQ的取值范围转化为求MP的取值范围是解决第(2)小题的关键.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{120}{x+2}$+3=$\frac{120}{x}$ | B. | $\frac{120}{x}$=$\frac{120}{x+2}$-3 | C. | $\frac{120}{x-2}$=$\frac{120}{x}$+3 | D. | $\frac{120}{x-2}$=$\frac{120}{x}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
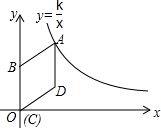 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为(4,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com