
 如图,在△ABC中,AB⊥BC,将△ABC沿着AC折叠,得到△ADC,点M、N分别在AB、AD边上,且AM=AN=$\frac{1}{3}$AB,连接MN,若∠BAD=60°,则tan∠MNC的值为3$\sqrt{3}$.
如图,在△ABC中,AB⊥BC,将△ABC沿着AC折叠,得到△ADC,点M、N分别在AB、AD边上,且AM=AN=$\frac{1}{3}$AB,连接MN,若∠BAD=60°,则tan∠MNC的值为3$\sqrt{3}$. 分析 如图,作辅助线;设BC=λ,分别用λ表示CP、AP、BD的长度;运用△AMN∽△ABD,列出比例式,求出AO、NO的长度,进而求出CO的长度;运用正切函数的定义即可解决问题.
解答  解:如图,连接BD;由题意得:
解:如图,连接BD;由题意得:
MN∥BD,MN⊥AC,BD⊥AC;∠BAC=$\frac{1}{2}$∠BAD=30°;
设BC=λ;在直角△ABC中,∵∠BAC=30°,
∴AC=2BC=2λ;而BC=DC,
∴∠CBD=∠CDB=$\frac{180°-120°}{2}$=30°,
∴CP=$\frac{1}{2}$λ,AP=2λ$-\frac{1}{2}λ$=$\frac{3}{2}λ$;BD=2BP=$\sqrt{3}$λ;
∵MN∥BD,
∴△AMN∽△ABD,
∴$\frac{AM}{AB}=\frac{AO}{AP}$=$\frac{MN}{BD}$,而AM=$\frac{1}{3}$AB,
∴AO=$\frac{1}{3}$AP=$\frac{1}{2}$λ,MN=$\frac{1}{3}$BD=$\frac{\sqrt{3}}{3}λ$;
∴NO=$\frac{1}{2}$MN=$\frac{\sqrt{3}}{6}λ$,
∴tan∠MNC=$\frac{CO}{NO}$,而CO=2λ$-\frac{1}{2}λ$=$\frac{3}{2}λ$,
∴tan∠MNC=3$\sqrt{3}$,
故答案为3$\sqrt{3}$.
点评 该题以直角三角形为载体,主要考查了直角三角形的边角关系、相似三角形的判定及其性质、三角函数的定义等知识点及其应用问题;灵活运用直角三角形的边角关系、相似三角形的判定及其性质等几何知识点是解题的基础和关键.


科目:初中数学 来源: 题型:选择题
| A. | 经过点(2,2) | B. | y随x的增大而增大 | ||
| C. | 两个分支分布在二、四象限 | D. | 图象关于x轴对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BC=$\sqrt{3}$,以BC为边作矩形ABCD,使∠DBC=30°,得BD=2,再以BD为边作矩形BDD1F,使∠DBD1=30°,得BD1=$\frac{4}{3}\sqrt{3}$,…,依此法继续作下去,则BD4的长为( )
如图,BC=$\sqrt{3}$,以BC为边作矩形ABCD,使∠DBC=30°,得BD=2,再以BD为边作矩形BDD1F,使∠DBD1=30°,得BD1=$\frac{4}{3}\sqrt{3}$,…,依此法继续作下去,则BD4的长为( )| A. | $\frac{16}{3}\sqrt{3}$ | B. | $\frac{32}{9}$ | C. | $\frac{{32\sqrt{3}}}{9}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
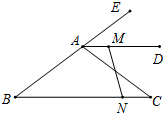 如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com