
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=![]() .
.
(1)求证:![]() ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
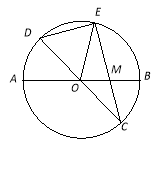
【答案】(1)证明:连接AC、EB
∵∠A=∠BEC,∠B=∠ACE
∴△AMC∽△EMB
∴![]()
∴![]() --------------------------------------------------------3分
--------------------------------------------------------3分
(2)解:∵DC是⊙O的直径
∴∠DEC=90°
∴![]()
∵DE=![]() ,CD=8,且EC为正数
,CD=8,且EC为正数
∴EC=7
∵M为OB的中点
∴BM=2,AM=6
∵![]() ,且EM>MC
,且EM>MC
∴EM=4------------------------------------------------------------------------------7分
(3)解:过点E作EF⊥AB,垂足为点F
∵OE=4,EM=4
∴OE=EM
∴OF=FM=1
∴EF=![]()
∴sin∠EOB=![]() ---------------------------------------------------------------------10分
---------------------------------------------------------------------10分
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.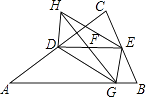
(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( ) 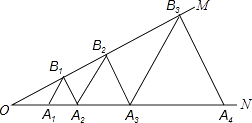
A.6
B.12
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨千米),铁路运价为1.2元/(吨千米),这两次运输共支出公路运费15 000元,铁路运费97200元. 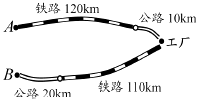
(1)求化工厂从A地购买这批原料及利用这批原料生产的产品各多少吨?
(2)计算这批产品的销售款比原料费和运输费的和多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0). 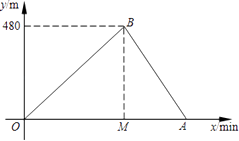
(1)A点所表示的实际意义是; ![]() =;
=;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查6个人中2个人生肖相同的概率,进行有放回地摸球试验,则( )
A. 用12个球每摸6次为一次试验,看是否有2次相同
B. 用12个球每摸12次为一次试验,看是否有2次相同
C. 用6个球每摸12次为一次试验,看是否有2次相同
D. 用6个球每摸6次为一次试验,看是否有2次相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于投针实验的说法正确的是( )
A. 针与平行线相交和不相交的可能性是相同的
B. 针与平行线相交的概率与针的长度没有关系
C. 实验次数越多,估算针与平行线相交的概率越精确
D. 针与平行线相交的概率不受两平行线间距离的影响
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是; 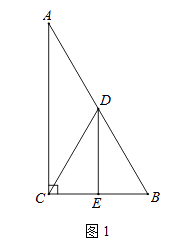
(2)如图2,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论; 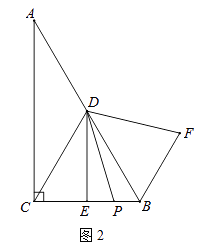
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系. 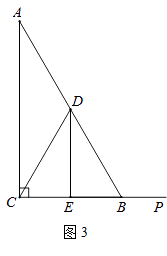
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE= ![]() ∠AOC.
∠AOC. 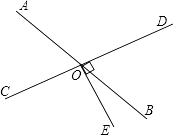
(1)指出与∠BOD相等的角,并说明理由;
(2)求∠BOD,∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com