

分析 (1)利用三角形的中位线得出PM=$\frac{1}{2}$CE,PN=$\frac{1}{2}$BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
(2)先判断出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=$\frac{1}{2}$BD,PN=$\frac{1}{2}$BD,即可得出PM=PN,同(1)的方法即可得出结论;
(3)方法1、先判断出MN最大时,△PMN的面积最大,进而求出AN,AM,即可得出MN最大=AM+AN,最后用面积公式即可得出结论.
方法2、先判断出BD最大时,△PMN的面积最大,而BD最大是AB+AD=14,即可.
解答 解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=$\frac{1}{2}$BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=$\frac{1}{2}$CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN,
(2)由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
同(1)的方法,利用三角形的中位线得,PN=$\frac{1}{2}$BD,PM=$\frac{1}{2}$CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形,
(3)如图2, 同(2)的方法得,△PMN是等腰直角三角形,
同(2)的方法得,△PMN是等腰直角三角形,
∴MN最大时,△PMN的面积最大,
∴DE∥BC且DE在顶点A上面,
∴MN最大=AM+AN,
连接AM,AN,
在△ADE中,AD=AE=4,∠DAE=90°,
∴AM=2$\sqrt{2}$,
在Rt△ABC中,AB=AC=10,AN=5$\sqrt{2}$,
∴MN最大=2$\sqrt{2}$+5$\sqrt{2}$=7$\sqrt{2}$,
∴S△PMN最大=$\frac{1}{2}$PM2=$\frac{1}{2}$×$\frac{1}{2}$MN2=$\frac{1}{4}$×(7$\sqrt{2}$)2=$\frac{49}{2}$.
方法2、由(2)知,△PMN是等腰直角三角形,PM=PN=$\frac{1}{2}$BD,
∴PM最大时,△PMN面积最大,
∴点D在AB的延长线上,
∴BD=AB+AD=14,
∴PM=7,
∴S△PMN最大=$\frac{1}{2}$PM2=$\frac{1}{2}$×72=$\frac{49}{2}$
点评 此题是几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质,解(1)的关键是判断出PM=$\frac{1}{2}$CE,PN=$\frac{1}{2}$BD,解(2)的关键是判断出△ABD≌△ACE,解(3)的关键是判断出MN最大时,△PMN的面积最大,是一道中考常考题.


科目:初中数学 来源: 题型:选择题
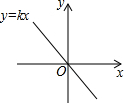 已知函数y=kx的图象如图所示,则对一元二次方程x2+x+k-1=0根的情况,说法正确的是( )
已知函数y=kx的图象如图所示,则对一元二次方程x2+x+k-1=0根的情况,说法正确的是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,图1是一个边长为a的正方形剪去一个边长为1的小正方形,图2是一个边长为(a-1)的正方形,记图1,图2中阴影部分的面积分别为S1,S2,则$\frac{{S}_{1}}{{S}_{2}}$可化简为$\frac{a+1}{a-1}$.
如图所示,图1是一个边长为a的正方形剪去一个边长为1的小正方形,图2是一个边长为(a-1)的正方形,记图1,图2中阴影部分的面积分别为S1,S2,则$\frac{{S}_{1}}{{S}_{2}}$可化简为$\frac{a+1}{a-1}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
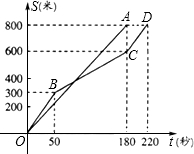 在今年我县初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小英和小西所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,如图,下列说法正确的是( )
在今年我县初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小英和小西所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,如图,下列说法正确的是( )| A. | 小英的速度随时间的增大而增大 | |
| B. | 小西的平均速度比小英的平均速度大 | |
| C. | 在起跑后180秒时,两人相遇 | |
| D. | 在起跑后50秒时,小西在小英的前面 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
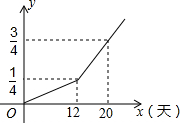 甲、乙两个工程队共同完成一项工程,先由甲单独做,然后乙队加入,两个工程队合作完成余下工程,工程的进度y与甲工作的时间x(天)的函数关系如图所示,则乙队单独完成此项工程需24天.
甲、乙两个工程队共同完成一项工程,先由甲单独做,然后乙队加入,两个工程队合作完成余下工程,工程的进度y与甲工作的时间x(天)的函数关系如图所示,则乙队单独完成此项工程需24天.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发4.68小时候再与轿车相遇(结果精确到0.01).
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发4.68小时候再与轿车相遇(结果精确到0.01).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com