
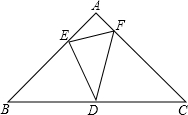
 △ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上.点E在AB上,点F在AC上,∠EDF=45°,给出以下结论:
△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上.点E在AB上,点F在AC上,∠EDF=45°,给出以下结论:| A. | ①②③ | B. | ①③④⑤ | C. | ②③④ | D. | ③④⑤ |
分析 ①根据等腰直角三角形的性质,可得BD的长度,∠B与∠C的大小,根据三角形的内角和,可得∠BDE的度数,根据三个角的和是平角,可得∠FDC的度数,可得∠DFC的度数,根据等腰三角形的判定,可得CF的长,根据正弦函数,可得DC边上的高,根据三角形的面积公式,可得答案;
②根据平角的定义得到∠EDB+∠FDC=135°,然后根据三角形的内角和得到∠DFC+∠FDC=135°,从而证得结论;
③证得△BDE∽△CFD后得到$\frac{BD}{FC}=\frac{BE}{CD}$,从而转化为比例式即可得到结论;
④根据勾股定理可得EF的长,根据三角形的周长,可得答案;
⑤根据三角形面积间的关系,可得答案.
解答 解:①由△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,得BC=2,点D位于边BC的中点上,得BD=DC=BE=1,∠B=∠C=45°,∠BDE=67.5°,∠EDF=45°,∴∠FDC=∠DFC=67.5°,CF=CD=1,DC边上的高是$\frac{\sqrt{2}}{2}$,S△CDF=$\frac{\sqrt{2}}{2}$,故①正确;
②∵∠EDF=45°,
∴∠EDB+∠FDC=135°,
∵∠B=∠C=45°,
∴∠DFC+∠FDC=135°,
∴∠BDE=∠DFC,故②正确;
③∠B=∠C,∠BED=∠FDC,
∴△BDE∽△CFD,
∴$\frac{BD}{FC}=\frac{BE}{CD}$
∴CF•BE=BD•CD=1,①故③正确;
④AE=AE=$\sqrt{2}$-1,EF=$\sqrt{2}$($\sqrt{2}$-1),C△AEF=$\sqrt{2}$,故④正确;
⑤S△AFE=$\frac{3}{2}-\sqrt{2}$,S△BDE=S△CDF=$\frac{\sqrt{2}}{2}$,S△DEF=1-($\frac{3}{2}-\sqrt{2}$)-$\sqrt{2}$=-$\frac{1}{2}$,S△AEF+2S△DEF=$\frac{3}{2}-\sqrt{2}$+2×(-$\frac{1}{2}$)=$\frac{1}{2}-\sqrt{2}$,故⑤错误.
故选:C.
点评 本题考查了相似三角形的判定与性质,利用了三角形边角间的关系,三角形的面积公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1333 | B. | 1999 | C. | 2001 | D. | 2249 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
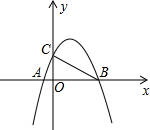 二次函数y=一x2+ax+b图象与x轴交于A($-\frac{1}{2}$,0),B(2,0)两点,且与y轴交于点C.
二次函数y=一x2+ax+b图象与x轴交于A($-\frac{1}{2}$,0),B(2,0)两点,且与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
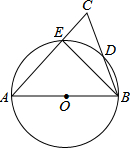 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
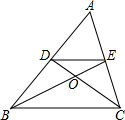 如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )
如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )| A. | 1:3 | B. | 1:9 | C. | 2:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com