
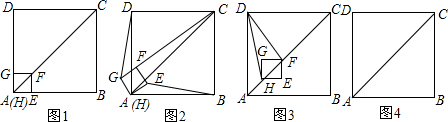
分析 (1)由正方形的性质可知:AD=AB,AG=AE,从而可得到DG=EB;由AC=$\sqrt{2}AD$,AF=$\sqrt{2}AG$,可知:FC=AC-AF=$\sqrt{2}AD-\sqrt{2}AG$,从而可求得答案;
(2)连接AF,由旋转的性质可知∠BAE=∠DAG,从而可证明△DGA≌△BEA,故此DG=BE,由旋转的性质可知∠CAF=∠DAG,根据对应边成比例且夹角相等的两三角形相似可证明△DGA∽△CFA,由相似三角形的性质可求得$\frac{CF}{DG}=\sqrt{2}$;
(3))①如图3所示:连接BD交AC于点O.先求得OD$\frac{5\sqrt{2}}{2}$和HF=$\sqrt{2}$,从而可知:HF<DH,HF<DF,故此DH=DF,由等腰三角形三线合一的性质可知:OH=OF,然后由OA=OC可得到AH=FC=2$\sqrt{2}$,由t=$\frac{AH}{\sqrt{2}}$可求得t=2;②如图4所示:连接BD交AC于点O.由△△DHF为等边三角形可知:∠HDO=30°,由特殊锐角三角函数值可知:OH=$\frac{\sqrt{3}}{3}DO$,从而可得到HF=$\frac{\sqrt{6}a}{3}$,然后再根据HF=$\sqrt{2}b$可求得:$\frac{b}{a}=\frac{\sqrt{3}}{3}$.
解答 解:(1)如图1所示: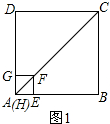
∵四边形ABCD与四边形EFGH均为正方形,
∴AD=AB,AG=AE.
∴AD-AG=AB-AE,即DG=EB.
∵AC=$\sqrt{2}AD$,$AF=\sqrt{2}AG$,
∴FC=AC-AF=$\sqrt{2}AD-\sqrt{2}AG$=$\sqrt{2}(AD-AG)$.
∴$\frac{CF}{DG}=\frac{\sqrt{2}(AD-AG)}{AD-AG}$=$\sqrt{2}$.
故答案为:DG=EB;$\sqrt{2}$.
(2)成立.
理由:如图2所示,连接AF.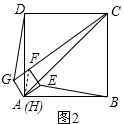
由旋转的性质可知:∠BAE=∠DAG.
在△DGA和△BEA中,$\left\{\begin{array}{l}{AD=AB}\\{∠DAG=∠BAE}\\{AG=AE}\end{array}\right.$,
∴△DGA≌△BEA.
∴DG=BE.
∵AF:AG=$\sqrt{2}$,AC:AD=$\sqrt{2}$,
∴$\frac{AF}{AG}=\frac{AC}{AD}$.
由旋转的性质可知:∠CAF=∠DAG
∴△DGA∽△CFA.
∴$\frac{FC}{DG}=\frac{AC}{AD}=\sqrt{2}$.
(3)①如图3所示:连接BD交AC于点O.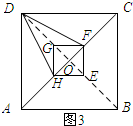
由正方形的性质可知:OD⊥AC,OD=$\frac{1}{2}BD$=$\frac{1}{2}×\sqrt{2}×AB=\frac{5\sqrt{2}}{2}$,
由垂线段最短可知:DF>OD,DH>OD.
又∵HF=$\sqrt{2}HE$=$\sqrt{2}$,
∴HF<DH,HF<DF.
∵△DHF为等腰三角形,
∴DH=DF.
∵DH=DF,DO⊥HF,
∴OH=OF.
又∵OA=OC,
∴AH=FC.
∴AH=FC=$\frac{1}{2}(AC-FH)$=$\frac{1}{2}×(5\sqrt{2}-\sqrt{2})$=2$\sqrt{2}$.
∴t=$\frac{2\sqrt{2}}{\sqrt{2}}$=2.
∴当t=2s时,△DFH为等腰三角形.
②存在.
理由:如图4所示:连接BD交AC于点O.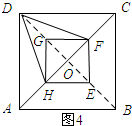
∵△DHF为等腰三角形,
∴DH=DH.
∵DH=DF,DO⊥AC,
∴∠HDO=$\frac{1}{2}$∠HDF=$\frac{1}{2}×60°$=30°.
∴OH=$\frac{\sqrt{3}}{3}DO$.
∴HF=$\frac{\sqrt{3}}{3}DB=\frac{\sqrt{3}}{3}×\sqrt{2}×a$=$\frac{\sqrt{6}a}{3}$.
∵HF=$\sqrt{2}b$,
∴$\frac{\sqrt{6}a}{3}=\sqrt{2}b$.
∴$\frac{b}{a}=\frac{\sqrt{3}}{3}$.
点评 本题主要考查的是正方形的性质、全等三角形的性质和判定、相似三角形的性质和判定、等腰三角形的性质、等腰三角形的性质、特殊锐角三角形函数值、图形的旋转和平移,熟练掌握相关图形的性质是解答本题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
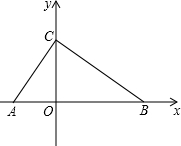 已知:在平面直角坐标系中,点O为坐标原点,△ABC的顶点A(-2,0),点B、C分别在x轴正半轴上和y轴正半轴上,∠ACB=90°,∠BAC=60°.
已知:在平面直角坐标系中,点O为坐标原点,△ABC的顶点A(-2,0),点B、C分别在x轴正半轴上和y轴正半轴上,∠ACB=90°,∠BAC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
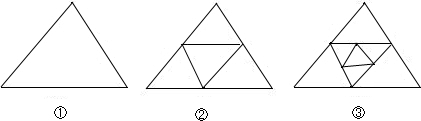
| 图形编号 | ① | ② | ③ | ④ | ⑤ | … |
| 三角形个数 | 1 | 5 | 9 | 13 | 17 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com