
【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,且∠CDE=20°,现将△CDE沿直线DE折叠得到△FDE,连结BF.∠BFE的度数是.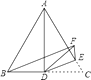
【答案】80°
【解析】∵△ABC是等边三角形,
∴∠C=60°,
又∵AD是BC边上的中线,
∴BD=CD,
又∵△CDE沿直线DE折叠得到△FDE,∠CDE=20°,
∴CD=DF,∠C=∠DFE=60°,∠CDE=∠FDE=20°,
∴BD=DF,∠CDF=40°,
∴∠DBF=∠DFB,
又∵∠CDF=∠DBF+∠DFB=40°,
∴∠DFB=![]() ∠CDF=
∠CDF=![]() ×40°=20°,
×40°=20°,
∴∠BFE=∠BFD+∠DFE=20°+60°=80°,
所以答案是:80°.
【考点精析】掌握三角形的外角和等腰三角形的性质是解答本题的根本,需要知道三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等腰三角形的两个底角相等(简称:等边对等角).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
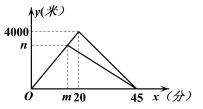
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
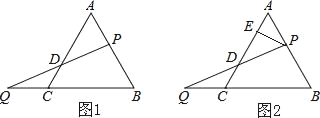
【题目】P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形两边中点的连线叫做这个三角形的中位线.只要顺次连结三角形三条中位线,则可将原三角形分割为四个全等的小三角形(如图(1));把三条边分成三等份,再按照图(2)将分点连起来,可以看作将整个三角形分成9个全等的小三角形;把三条边分成四等份,…,按照这种方式分下去,第n个图形中应该得到( )个全等的小三角形.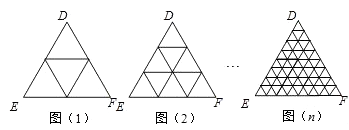
A.![]()
B.![]()
C.![]()
D.(n+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AE是经过A点的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,CE=2,BD=6,则DE的长为.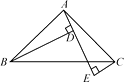
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
A.当x>1时y随x的增大而增大
B.抛物线的对称轴为x= ![]()
C.当x=2时y=-1
D.方程ax2+bx+c=0一个负数解x1满足-1<x1<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() (a是常数,
(a是常数, ![]() ),下列结论正确的是( )
),下列结论正确的是( )
A.当a = 1时,函数图像经过点(一1,0)
B.当a = 一2时,函数图像与x轴没有交点
C.若 ![]() ,函数图像的顶点始终在x轴的下方
,函数图像的顶点始终在x轴的下方
D.若 ![]() ,则当
,则当 ![]() 时,y随x 的增大而增大
时,y随x 的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com