
分析 (1)根据月销售量为=500-(销售单价-50)×10,即可得出结论,再根据月销售利润=销售每千克的利润×销售数量,代入数据即可得出结论;
(2)根据月销售利润=销售每千克的利润×销售数量,即可得出y与x之间的函数关系式;
(3)令y=-10x2+1400x-40000=8000,解一元二次方程即可得出x的值,再根据月销售成本不超过10000元即可得出关于x的一元一次不等式,解之即可得出x的取值范围,由此即可确定x的值.
解答 解:(1)当销售单价定为每千克55元时,月销售量为500-(55-50)×10=450(千克),
月销售利润为(55-40)×450=6750(元).
故答案为:450;6750.
(2)根据题意得:y=(x-40)[500-(x-50)×10]=-10x2+1400x-40000.
(3)当y=8000时,有-10x2+1400x-40000=8000,
解得:x1=80,x2=60.
∵x[500-(x-50)×10]=400(100-x)≤10000,
解得:x≥75,
∴x=80.
答:销售单价定为80元.
点评 本题考查了一元二次方程的应用以及解一元一次不等式,根据数量关系列出一元二次方程(或列式计算)是解题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
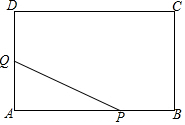 如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,
如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
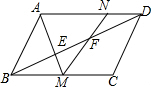 如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.
如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com