练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知两圆的半径长是方程（x-3）（x-7）=0的两个解，且两圆的圆心距为d，若两圆相离，则下列结论正确的是（　　）
    A．0＜d＜4B．d＞10C．0≤d＜4或d＞10D．4＜d＜10

    分析 首先解方程求得两圆的半径，然后根据两圆相离分外离和内含两种情况分类讨论得到答案即可．

    解答 解：∵两圆的半径长是方程（x-3）（x-7）=0的两个解，
    解得：x=3或x=7，
    ∴两圆的半径分别为3和7，
    ∵两圆相离，
    ∴当两圆外离时，d＞R+r
    即：d＞10，
    当两圆内含时，0≤d＜R-r，
    即：0≤d＜4，
    故选C．

    点评 本题考查了圆与圆的位置关系，解题中能分外离和内切讨论是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．已知x2+2x-4=0，求代数式2（x-1）2-x（x-6）+3的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

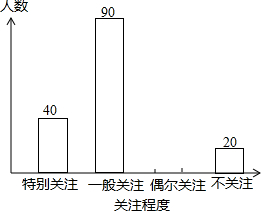    13．第33届“中国洛阳牡丹文化节”于2015年4月1日-5月5日在文明古都洛阳举行，某初中学校为了了解本校2500名学生对此次文化节的关注程度，随机抽取了200名学生进行调查，按关注程度绘成了条形统计图（如图）．已知一般关注的人数占被调查人数的45%．
    （1）补全条形统计图；
    （2）如果把“特别关注”、“一般关注”、“偶尔关注”都统计成关注．那么全校关注本届牡丹文化节的学生大约有多少名？
    （3）该校计划组织志愿者服务小组参与牡丹文化节服务活动，准备从特别关注中的3名男生小亮、小明、小伟和2名女生小丽、小敏中选取一名男生和一名女生参加学校志愿者服务小组．
    ①若随机选取一名男生和一名女生参加志愿者服务小组，请用树状图或列表法写出所有可能出现的结果；
    ②求出恰好选中男生小明与女生小丽的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

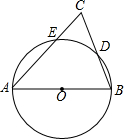    10．如图，AB为⊙O的直径，AC交⊙O于E点，BC交⊙O于D点，CD=BD．∠C=70°，以下四个结论中错误的是（　　）
    A．AC=ABB．$\widehat{DE}$=$\widehat{BD}$C．∠A=45°D．$\frac{CE}{CD}$=$\frac{CB}{CA}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）作图发现
    如图1，已知△ABC，小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE．连接BE，CD．这时他发现BE与CD的数量关系是相等．
    （2）拓展探究
    如图2．已知△ABC，小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，试判断BE与CD之间的数量关系，并说明理由．
    （3）解决问题
    如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=200米．AC=AE，则BE=200$\sqrt{3}$米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．若∠α补角加上30°是∠α余角的3倍，则∠α=30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．用科学记数法表示21345为2.13×104（保留三位有效数字）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

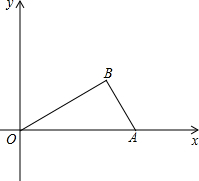    11．如图，在平面直角坐标系中，Rt△ABO的斜边OA在x轴上，点B在第一象限内，AO=4，∠BOA=30°．点C（t，0）是x轴正半轴上一动点（t＞0且t≠4）：
    （1）点B的坐标为（3，$\sqrt{3}$）；过点O、B、A的抛物线解析式为y=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x；
    （2）作△OBC的外接圆⊙P，当圆心P在（1）中抛物线上时，求点C和圆心P的坐标；
    （3）设△OBC的外接圆⊙P与y轴的另一交点为D，请将OD用含t的代数式表示出来，并求CD的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，已知在⊙O中，AB=CD=EF=HG，BC=DE=FG=AH，则∠AHG的度数是（　　）
    A．120°B．125°C．130°D．135°

    查看答案和解析>>

    同步练习册答案