(1)∵k为(m-2)x
2-(m-1)x+m=0的实数根,
∴(m-2)k
2-(m-1)k+m=0.+
①当k=m时,
∵k为非零实数根,
∴m≠0,方程两边都除以m,得(m-2)m-(m-1)+1=0.
整理,得m
2-3m+2=0.
解得m
1=1,m
2=2.
∵(m-2)x
2-(m-1)x+m=0是关于x的一元二次方程,
∴m≠2.
∴m=1.
②∵k为原方程的非零实数根,
∴将方程两边都除以k,得
(m-2)k-(m-1)+=0.
整理,得
m(k+)-2k=m-1.
∴
y=m(k+)-2k+5=m+4.
(2)解法一:△=[-(m-1)]
2-4m(m-2)=-3m
2+6m+1=-3m(m-2)+1.
当
<m<2时,m>0,m-2<0.
∴-3m(m-2)>0,-3m(m-2)+1>1>0,△>0.
∴当
<m<2时,此方程有两个不相等的实数根.
解法二:直接分析
<m<2时,函数y=(m-2)x
2-(m-1)x+m的图象,
∵该函数的图象为抛物线,开口向下,与y轴正半轴相交,
∴该抛物线必与x轴有两个不同交点.
∴当
<m<2时,此方程有两个不相等的实数根.
解法三:△=[-(m-1)]
2-4m(m-2)=-3m
2+6m+1=-3(m-1)
2+4.
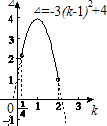
结合△=-3(m-1)
2+4关于m的图象可知,(如图)
当
<m≤1时,
<△≤4;
当1<m<2时,1<△<4.
∴当
<m<2时,△>0.
∴当
<m<2时,此方程有两个不相等的实数根.




 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案