
【题目】(1)如图1,在![]() 中,分别以
中,分别以![]() 、
、![]() 为斜边,向
为斜边,向![]() 的形外作等腰直角三角形,直角的顶点分别为
的形外作等腰直角三角形,直角的顶点分别为![]() ,点
,点![]() 分别为
分别为![]() 边的中点.问:
边的中点.问: ![]() 是否全等?____(填“是”或“否”);
是否全等?____(填“是”或“否”);
(2)如图2,在![]() 中,分别以
中,分别以![]() 为底边,向
为底边,向![]() 的形外作等腰三角形,顶角的顶点分别为
的形外作等腰三角形,顶角的顶点分别为![]() ,且
,且![]() .点
.点![]() 分别为
分别为![]()
![]() 边的中点.
边的中点.
①试判断![]() 是否满足(1)中的关系?若满足,请说明理由;若不满足,请写
是否满足(1)中的关系?若满足,请说明理由;若不满足,请写![]() 之间存在的一种关系,并加以说明.
之间存在的一种关系,并加以说明.
②若![]() ,
, ![]() ,
, ![]() 的面积为32,求
的面积为32,求![]() 的面积.
的面积.

【答案】(1)是;(2)①否, ![]() 相似,理由见解析;②
相似,理由见解析;②![]() .
.
【解析】试题分析:
(1)由已知条件易证:DF=AF=GM,FM=AG=GE,∠DFB=∠EGC=90°,∠BFM=∠BAC=∠MGC,从而可得∠DFM=∠EGM,由此即可由“SAS”证得△DFM≌△MGE;
(2)①同(1)可证得∠DFM=∠MGE,由∠BAD+∠CAE=90°,结合∠AGE=90°,可证得∠DAF=∠AEG,从而可得tan∠DAF=tan∠AEG,由此可得![]() ,结合AF=GM,AG=FM可得
,结合AF=GM,AG=FM可得![]() ,这样即可证得△DFM∽△MGE了;
,这样即可证得△DFM∽△MGE了;
②由AB=6易得AF=MG=3,结合AD=5,在Rt△ADF中易得DF=4,从而可得DF:MG=4:3,结合△DFM∽△MGE即可由△DFM的面积求得△MGE的面积了.
试题解析:
(1)是,理由如下:
∵△ABD、△AEC分别是以AB和AC为斜边的等腰直角三角形,点F、M、G分别是AB、BC、AC的中点,
∴DF=AF=GM,FM=AG=GE,∠DFB=∠EGC=90°,FM∥AC,MG∥AB,
∴∠BFM=∠BAC=∠MGC,
∴∠DFB+∠BFM=∠MGC+∠EGC,即∠DFM=∠EGM,
∴△DFM≌△MGE;
故答案为:“是”;
(2)①否, ![]() 相似;
相似;
理由:∵![]() 都是等腰三角形,且
都是等腰三角形,且![]() 为
为![]() 的中点,
的中点,
∴![]() ,∵点
,∵点![]() 分别为
分别为![]() 边的中点,
边的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∵由①知![]() ,且
,且![]() 的面积为32,
的面积为32,
∴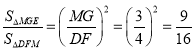 ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】合肥市打造世界级国家旅游中心,精心设计12个千年古镇。如图1是某明清小院围墙中的精美图案,它是两个形状大小相同的菱形与一个圆组成,且A、C、E、G在其对称轴AG上.已知菱形的边长和圆的直径都是1dm,∠A= 60°.

(1)求图案中AG的长;
(2)假设小院的围墙一侧用上述图案如图2排列,其中第二块图案左边菱形一个顶点正好经过第一块图案的右边菱形的对称中心,....,以此类推,第101块这种图案这样排列长为多少m?(不考虑缝隙及拼接处)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某升降机第一次上升5米,第二次又上升6米,第三次下降4米,第四次又下降7米。(上升记为正,下降记为负,单位:米)
(1)这时升降机与初始位置相距多少米?
(2)升降机共运行了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=x+m的图象与反比例函数![]() 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.

(1)求一次函数的解析式;
(2)已知双曲线在第一象限上有一点C到y轴的距离为3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,射线
,射线![]() 从
从![]() 的位置开始绕点
的位置开始绕点![]() 按顺时针方向旋转,速度是每秒
按顺时针方向旋转,速度是每秒![]() ,同时射线
,同时射线![]() 从
从![]() 的位置开始绕点
的位置开始绕点![]() 按逆时针方向旋转,速度是每秒
按逆时针方向旋转,速度是每秒![]() ,设旋转时间为
,设旋转时间为![]() 秒
秒![]() .
.
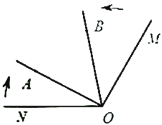
(1)用含![]() 的代数式表示
的代数式表示![]() 和
和![]() 的度数;
的度数;
(2)在旋转过程中,当![]() 等于
等于![]() 时,求
时,求![]() 的值;
的值;
(3)在旋转过程中是否存在这样的![]() ,使得射线
,使得射线![]() 恰好是图中某个角的平分线?如果存在,请求出
恰好是图中某个角的平分线?如果存在,请求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是直线AB上一点,∠BOC<90°,三角板(MON)的直角顶点落在点O处现将三角板绕着点O旋转,并保持OM和OC在直线AB的同一侧.
(1)若∠BOC=50°
①当OM平分∠BOC时,求∠AON的度数.
②当OM在∠BOC内部,且∠AON=3∠COM时,求∠CON的度数:
(2)当∠COM=2∠AON时,请画出示意图,猜想∠AOM与∠BOC的数量关系,并说明理由.
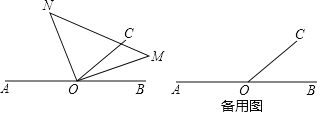
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com