
����Ŀ������ʦ�Լݽγ��ظ��ٹ�·��A�ص�B�����Σ�;�������纣���ţ�������4.5Сʱ������ʱƽ���ٶ������10ǧ��/Сʱ����ȥʱ�����˰�Сʱ�ص�A�أ�
��1����A��B���ؼ��·�̣�
��2�������纣���ŵij��ȼ����ŷѼ�����

��ʡ��ͨ���Ź涨���γ��ĸ��ٹ�·ͨ�з�y��Ԫ���ļ��㷽��Ϊ��y=ax+b+5������a��Ԫ/ǧ�ף�Ϊ���ٹ�·��̷ѣ�x��ǧ�ף�Ϊ���ٹ�·��̣��������纣���ų�����b��Ԫ��Ϊ�纣���Ź��ŷѣ�������ʦ��A�ص�B�������ĸ��ٹ�·ͨ�з�Ϊ295.4Ԫ����γ��ĸ��ٹ�·��̷�a��
���𰸡���1��360ǧ����2��0.4Ԫ/ǧ��
��������
�����������1������������ʱ�䡢�ٶȺ�·�̿ɵõ�һ��һԪһ�η��̣���˷��̿ɵ�A��B���ؼ�ĸ��ٹ�··�̣�
��2�����ݱ��������ʦ��A��B�����ĸ��ٹ�·ͨ�зѿ��Խ�����ʽy=ax+b+5ת����һ������δ֪��a��һԪһ�η��̣���˷��̿ɵýγ��ĸ��ٹ�·��̷ѣ�
�⣺��1����A��B���ؼ�ĸ��ٹ�··��Ϊsǧ�ף�������ã�
![]() ��
��![]() =10��
=10��
4.5s��4s=180��
0.5s=180��
���s=360��
����A��B���ؼ�ĸ��ٹ�··��Ϊ��360ǧ�ף�
��2���γ��ĸ��ٹ�·ͨ�з�y��Ԫ���ļ��㷽��Ϊ��y=ax+b+5��
���ݱ��������ʦ��ͨ�зѿ�֪��
y=295.4��x=360��48��36=276��b=100+80=180�������Ǵ���y=ax+b+5�еã�
295.4=276a+180+5��
���a=0.4��
���Խγ��ĸ��ٹ�·��̷�Ϊ��0.4Ԫ/ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABN����ACMλ����ͼ��ʾ��AB=AC��AD=AE����1=��2��
��1����֤��BD=CE��
��2����֤����M=��N��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��1��3������B��m��1����һ�κ���![]() ��ͼ���ϵ����㣬һ�κ���
��ͼ���ϵ����㣬һ�κ���![]() ͼ����x�ύ�ڵ�D.
ͼ����x�ύ�ڵ�D.

��1��b = ��m = ��
��2������B��ֱ��l��ֱ��x�ᣬ��E�ǵ�D����ֱ��l�ĶԳƵ㣬��C�ǵ�A����ԭ��ĶԳƵ㣮���жϵ�B��E��C�Ƿ���ͬһ��ֱ���ϣ���˵�����ɣ�
��3������AO��BO������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������IJ�����װ��16��ֻ����ɫ��ͬ�������к�����x����������2x����������Ϊ�����ּ״Ӳ������������һ�������Ǻ������ͬѧ��ʤ����ͬѧ����������Żز����ȣ�����ͬѧ�������һ������Ϊ��������ͬѧ��ʤ��
��1����X=3ʱ��˭��ʤ�Ŀ����Դ�
��2����xΪ��ֵʱ����Ϸ��˫���ǹ�ƽ�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�P��Q�ֱ���BC��AC�ϵĵ㣬��PR��AB��PS��AC������ֱ���R��S����AQ=PQ��PR=PS�������ĸ����ۣ���AS=AR����QP��AR���ۡ�BRP�ա�QSP����AP��ֱƽ��RS��������ȷ���۵������ ���뽫������ȷ���۵���Ŷ����ϣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��3��2��������1��0���������߶�BA�Ƶ�B˳ʱ����ת90��õ��߶�BA�䣬���A�������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ�����3���ֱ�������֩�1��1��2��С�����dz�������ֲ�ͬ������������
��1������شӿڴ���ȡ��һС����ȡ����С���ϱ������Ϊ�����ĸ��ʣ�
��2������شӿڴ���ȡ��һС�Żغ���ȡ���ڶ���С��������ȡ�������ֵĺ͵���0�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣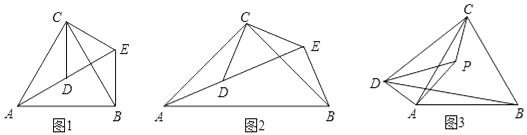
��1�����ⷢ�֣���ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ�����DCE��ת����A��D��E��ͬһֱ���ϣ�����BE����֤��BCE�ա�ACD����
�١�BEC=�㣻���߶�AD��BE֮���������ϵ�� ��
��2����չ�о���
��ͼ2����ACB�͡�DCE��Ϊ���������Σ��ҡ�ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ���AE=15��DE=7����AB�ij��ȣ�
��3��̽�����֣�
��ͼ3��PΪ�ȱߡ�ABC��һ�㣬�ҡ�APC=150�㣬�ҡ�APD=30�㣬AP=5��CP=4��DP=8����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵȱ������Σ���ֱ��AC��ֱ��BC�Ϸֱ�ȡ��D�͵���AD=CE��ֱ��BD��AE�ཻ�ڵ�F��
��1����ͼ1��ʾ������D����E�ֱ����߶�CA��BC��ʱ����֤��BD=AE��
��2����ͼ2��ʾ������D����E�ֱ���CA��BC���ӳ���ʱ�����BFE�Ķ�����
��3����ͼ3��ʾ���ڣ�2���������£�����C��CM��BD����EF�ڵ�M����DF��AF��AM=1��2��4��BC=12����CE�ij��ȣ�
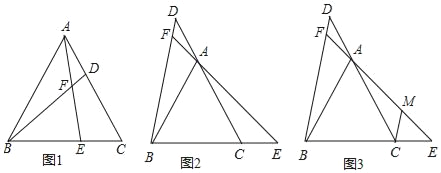
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com