
分析 (1)根据有理数的加减混合运算的运算方法,求出算式的值是多少即可.
(2)(3)(4)应用加法交换律和加法结合律,求出每个算式的值各是多少即可.
解答 解:(1)-7+11+4+(-2)
=4+4-2
=6
(2)-$\frac{1}{2}$-(-3$\frac{3}{4}$)-2$\frac{1}{2}$-(-1$\frac{1}{4}$)
=(-$\frac{1}{2}$-2$\frac{1}{2}$)+(3$\frac{3}{4}$+1$\frac{1}{4}$)
=-3+5
=2
(3)-2.4+3.5-4.6+3.5
=(-2.4-4.6)+(3.5+3.5)
=-7+7
=0
(4)(-8$\frac{3}{7}$)+(-7.5)-$\frac{4}{7}$+$\frac{1}{2}$
=(-8$\frac{3}{7}$-$\frac{4}{7}$)+(-7.5+$\frac{1}{2}$)
=-9-7
=-16
点评 此题主要考查了有理数的加减混合运算,要熟练掌握,注意运算顺序,注意加法运算定律的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
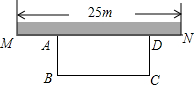 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知y与x-3成正比例,当x=4时,y=3.
已知y与x-3成正比例,当x=4时,y=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com