
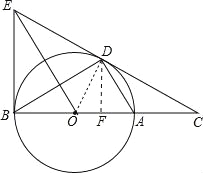
【题目】如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)若BC=8cm,tan∠CDA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)条件下,过点B作⊙O的切线交CD的延长线于点E,连接OE,求四边形OEDA的面积.
【答案】(1)证明见解析(2)3(3)12.6
【解析】
试题分析:(1)要证明CD是⊙O的切线,只需要连接OD,证明∠ODC=90°即可,由∠CDA=∠CBD,∠BDA=90°,OA=OD得到∠ODA=∠OAD,然后进行转化即可得到∠ODC=90°,本题得以解决;
(2)根据题意可以得到△CDA和△CBD相似,然后根据BC=8cm,tan∠CDA=![]() ,∠CDA=∠CBD,可以求得CD、CA的长,从而可以求得BA的长,进而可以得到⊙O的半径;
,∠CDA=∠CBD,可以求得CD、CA的长,从而可以求得BA的长,进而可以得到⊙O的半径;
(3)由题意可得,∠EBC=90°,可以证明△EBC和△ODC相似,从而可以求得EB的长,然后根据四边形OEDA的面积等于△EBC的面积减去△EBO的面积再减去△DAC的面积,从而可以得到四边形OEDA的面积,本题得以解决.
试题解析:(1)连接OD,如右图所示,
∵AB为⊙O的直径,
∴∠BDA=90°,
又∵OD=OA,∠CDA=∠CBD,
∴∠ODA=∠OAD,
∴∠CBD+∠OAD=180°﹣∠BDA=90°,
∴∠ODA+∠CDA=∠OAD+∠CDA=90°,
∴∠ODC=90°,
即CD是⊙O的切线;
(2)∵∠DCA=∠BCD,∠CDA=∠CBD,
∴△CDA∽△CBD,
∴![]() ,
,
又∵BC=8cm,tan∠CDA=![]() ,∠CDA=∠CBD,∠BDA=90°,
,∠CDA=∠CBD,∠BDA=90°,
∴tan∠CBD=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得,CD=4,CA=2,
∴BA=CB﹣CA=8﹣2=6,
∴OB=3,
即⊙O的半径是3cm;
(3)作DF⊥BC于点F,如右上图所示
由已知可得,∠ODC=∠EBC=90°,∠DCO=∠BCE,
∴△DCO∽△BCE,
∴![]() ,
,
∵OD=3,CD=4,CB=8,
∴EB=6,
又∵CO=CB﹣OB=8﹣3=5,OD=3,CD=4,∠ODC=90°,DF⊥OC,
∴![]() ,
,
解得DF=2.4,
∴![]() =
=![]() =
=![]() =12.6cm,
=12.6cm,
即四边形OEDA的面积是12.6cm2.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式;
(2)若MN与直线y=﹣2![]() x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:
x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:
①求证:BC平分∠MBN;
②求△MBC外心的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )
的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4, △ABC的面积是( )

A.21B.42C.56D.84
查看答案和解析>>
科目:初中数学 来源: 题型:
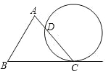
【题目】如图为![]() 和一圆的重迭情形,此圆与直线
和一圆的重迭情形,此圆与直线![]() 相切于
相切于![]() 点,且与
点,且与![]() 交于另一点
交于另一点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的度数为何( )
的度数为何( )
A. 50° B. 60° C. 100° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝新年的到来,我市某中学举行“青春飞扬”元旦汇演,正式表演前,把各班的节目分为A(戏类),B(小品类),C(歌舞类),D(其他)四个类别,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题.
(1)参加汇演的节目数共有 个,在扇形统计图中,表示“B类”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)学校决定从本次汇演的D类节目中,选出2个去参加市中学生文艺汇演.已知D类节目中有相声节目2个,魔术节目1个,朗诵节目1个,请求出所选2个节目恰好是一个相声和一个魔术概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接第十一届少数民族传统体育运动会,郑州市园林局打算购买A,B两种花装点城区道路,负责人小李去花卉基地调查发现:购买2盆A种花和3盆B种花需要23元,购买4盆A种花和2盆B种花需要26元.
(1)求A,B两种花的单价各为多少元?
(2)郑州市园林局若购买A, B两种花共12000盆,且购买的A种花不少于3000盆,但不多于5000盆,若购买的A种花不超于3000盆时,花卉基地会给每盆A种花打8折,
①设购买的A种花m盆,总费用为W元,求w与m的关系式:
②请你帮小李设计一种购花方案使花费总少?并求出最少费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
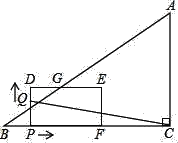
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,四边形PDEF是矩形,PD=2,PF=4,DE与AB边交于点G,点P从点B出发沿BC以每秒1个单位长的速度向点C匀速运动,伴随点P的运动,矩形PDEF在射线BC上滑动;点Q从点P出发沿折线PD﹣DE以每秒1个单位长的速度匀速运动.点P,Q同时出发,当点Q到达点E时停止运动,点P也随之停止.设点P,Q运动的时间是t秒(t>0)
(1)当t=1时,QD= ,DG= ;
(2)当点Q到达点G时,求出t的值;
(3)t为何值时,△PQC是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
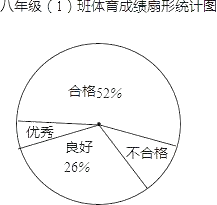
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com