
分析 (1)根据判别式的意义得到△=[-(2k+3)]2-4•1•k2=12k+9>0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2k+3,x1x2=k2,再把x1x2-x12-x22=-9变形为即3x1x2-(x1+x2)2=-9,则3k2-(2k+3)2=-9,然后解关于k的方程,最后利用k的范围确定满足条件的k的值.
解答 解:(1)由已知可得,△=[-(2k+3)]2-4•1•k2=12k+9>0
∴k>-$\frac{3}{4}$
(2)由已知可得x1+x2=2k+3,x1x2=k2,
∵x1x2-x12-x22=-9,
∴x1x2-[(x1+x2)2-2x1x2]=-9,
即3x1x2-(x1+x2)2=-9,
∴3k2-(2k+3)2=-9,
整理得k2+12k=0,解得k1=0,k2=-12,
又k>-$\frac{3}{4}$,
∴k=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


科目:初中数学 来源: 题型:解答题
 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪.如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
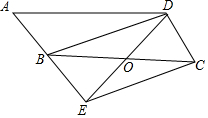 如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com