
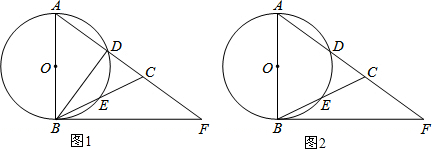
分析 (1)根据等腰三角形的性质和三角形内角和定理得到∠ABC=$\frac{1}{2}$(180°-∠CAB)=90°-$\frac{1}{2}$∠CAB,由于∠CAB=2∠CBF,则∠ABC+∠CBF=90°,则根据切线的判定定理得BF是⊙O的切线;
(2)先利用勾股定理计算出AF=10,再证明Rt△ABD∽Rt△AFB,然后利用相似比可计算出AD;
(3)作CH⊥BF于H,如图2,利用AC=AB=6可得CF=AF-AC=4,再证明△FCH∽△FAB,利用相似比可计算出CH=$\frac{12}{5}$,FH=$\frac{16}{5}$,则BH=BF-FH=$\frac{24}{5}$,然后在Rt△BHC中,利用正切的定义求解.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=$\frac{1}{2}$(180°-∠CAB)=90°-$\frac{1}{2}$∠CAB,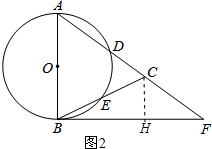
∵∠CAB=2∠CBF,
∴∠ABC=90°-∠CBF,即∠ABC+∠CBF=90°,
∴AB⊥BF,
∴BF是⊙O的切线;
(2)解:在Rt△ABF中,∵AB=6,BF=8,
∴AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=10,
∵∠DAB=∠BAF,
∴Rt△ABD∽Rt△AFB,
∴AD:AB=AB:AF,即AD:6=6:10,
∴AD=$\frac{18}{5}$;
(3)解:作CH⊥BF于H,如图2,
∵AC=AB=6,
∴CF=AF-AC=10-6=4,
∵CH∥AB,
∴△FCH∽△FAB,
∴$\frac{CH}{AB}$=$\frac{FH}{FB}$=$\frac{FC}{FA}$,即$\frac{CH}{6}$=$\frac{FH}{8}$=$\frac{4}{10}$,
∴CH=$\frac{12}{5}$,FH=$\frac{16}{5}$,
∴BH=BF-FH=8-$\frac{16}{5}$=$\frac{24}{5}$,
在Rt△BHC中,tan∠CBH=$\frac{CH}{BH}$=$\frac{\frac{12}{5}}{\frac{24}{5}}$=$\frac{1}{2}$,
即tan∠CBF的值为$\frac{1}{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:选择题
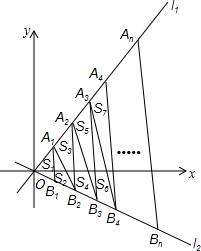 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
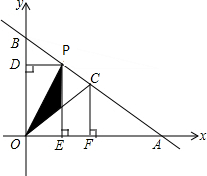 如图,点A,B坐标分别为(8,0)、(0,6),点C是线段AB的中点,点P是射线BA上一动点,过P作PD⊥y轴于D,PE⊥x轴于E,设OE=t,矩形OEPD与△POC重合部分的面积为S.
如图,点A,B坐标分别为(8,0)、(0,6),点C是线段AB的中点,点P是射线BA上一动点,过P作PD⊥y轴于D,PE⊥x轴于E,设OE=t,矩形OEPD与△POC重合部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
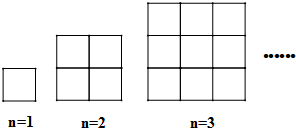
| A. | 220 | B. | 200 | C. | 120 | D. | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.
设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
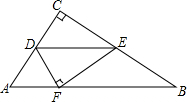 如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )| A. | 3.6 | B. | 4 | C. | 4.8 | D. | 6.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com