
【题目】如图1是长方形纸袋,将纸袋沿EF折叠成图2,再沿BF折叠成图3,若∠DEF=α,用α表示图3中∠CFE的大小为 _________ .
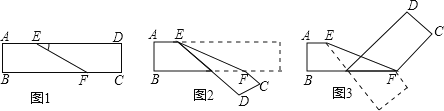
【答案】180°-3α.
【解析】
试题分析:先根据进行的性质得AD∥BC,则∠BFE=∠DEF=α,根据折叠的性质,把如图1中的方形纸袋沿EF折叠成图2,则∠MEF=α,把图2沿BF折叠成图3,则∠MFH=∠CFM,根据平行线的性质由FH∥MG得到∠MFH=180°-∠FMG,再利用三角形外角性质得∠FMG=∠MFE+∠MEF=2α,则∠MFH=180°-2α,所以∠CFM=180°-2α,然后利用∠CFE=∠CFM-∠EFM求解.
试题解析:
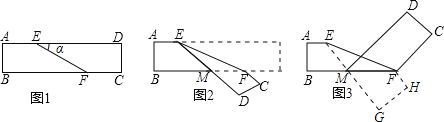
在图1中,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠BFE=∠DEF=α,
∵如图1中的方形纸袋沿EF折叠成图2,
∴∠MEF=α,
∵图2再沿BF折叠成图3,
∴在图3中,∠MFH=∠CFM,
∵FH∥MG,
∴∠MFH=180°-∠FMG,
∵∠FMG=∠MFE+∠MEF=α+α=2α,
∴∠MFH=180°-2α,
∴∠CFM=180°-2α,
∴∠CFE=∠CFM-∠EFM=180°-2α-α=180°-3α.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E. 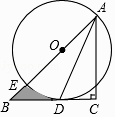
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 ![]() 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 
(1)求证:AP=BQ;
(2)当BQ=4 ![]() 时,求
时,求 ![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④ ![]() 为常量.其中正确的有 .
为常量.其中正确的有 . 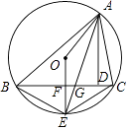
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.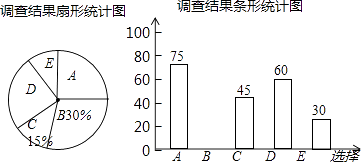
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 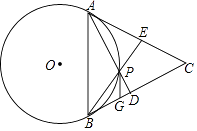
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) 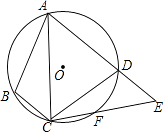
A.45°
B.50°
C.55°
D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com